Un étudiant propose la fonction recherche_dichotomie_bug1 ci-dessous pour effectuer une recherche par dichotomie de x dans la liste L. Vérifier que cette fonction ne se termine pas toujours.

def recherche_dichotomie_bug1(L, x):
    a, b = 0, len(L)-1
    while a < b:
        ind_m = len(L) // 2
        m = L[ind_m]
        if x == m:
            return True
        elif  x < m:
            b = ind_m
        else:
            a = ind_m
    return True

Un autre étudiant propose la fonction recherche_dichotomie_bug2 ci-dessous pour effectuer une recherche par dichotomie de x dans la liste L. Vérifier que cette fonction semble toujours se terminer mais qu'elle ne renvoie pas toujours le bon résultat.

def recherche_dichotomie_bug2(L, x):
    a, b = 0, len(L)-1
    while a < b:
        ind_m = (a+b) // 2
        m = L[ind_m]
        if x == m:
            return True
        elif  x < m:
            b = ind_m -1
        else:
            a = ind_m+1
        print(a, b)
    return True

Compléter la fonction expo_rapide suivante pour qu'elle retourne la puissance \(a^{n}\).

def expo_rapide(a, n):
    assert n >= 0
    res = ??
    while ??:
        if n % 2 == 0:
            a, n = a**2, n // 2
        else:
            res = ??
            a, n = a**2, n // 2
    return res

def expo_rapide(a, n):
    assert n >= 0
    res = 1
    while n > 0:
        if n % 2 == 0:
            a, n = a**2, n // 2
        else:
            res *= a
            a, n = a**2, n // 2
    return res

assert expo_rapide(3, 4) == 81
assert expo_rapide(2, 10) == 1024
assert expo_rapide(13, 0) == 1
assert expo_rapide(15, 1) == 15

Compléter maintenant la fonction expo_rapide_base_quatre pour qu'elle retourne la puissance \(a^{n}\).

def expo_rapide_base_quatre(a, n):
    assert n >= 0
    res = ??
    while ??:
        # n = 4q+r avec 0<=r<4
        q, r = n // 4, n % 4
        # a**(4q + r) = (a**4)**q * a**r
        n = ??
        res = ??
        a = ??
    return res

def expo_rapide_base_quatre(a, n):
    assert n >= 0
    res = 1
    while n > 0:
        n, r = n // 4, n % 4
        res *= a**r
        a = a**4
    return res

assert expo_rapide_base_quatre(3, 4) == 81
assert expo_rapide_base_quatre(2, 10) == 1024
assert expo_rapide_base_quatre(13, 0) == 1
assert expo_rapide_base_quatre(15, 1) == 15

Compléter la définition de la fonction my_sqrt ci-dessous afin qu'elle retourne un couple de flottants qui sont dans l'ordre une valeur approchée par défault et une valeur approchée par excès (toutes les deux à la precision demandée en second argument) de la racine carré de x en utilisant une méthode de dichotomie et uniquement des multiplications (la fonction sqrt est uniquement importée pour les tests qui suivent la fonction).

from math import sqrt

def my_sqrt(x, precision):
    assert ??
    a, b = ??
    while ??:
        m = ??
        if ??:
            ??
        else:
            ??
    return ??

precision = 1.e-14
for x in [0, 1, 2, 3.4, 101.]:
    val_def, val_exce = my_sqrt(x, precision)
    assert val_exce-val_def ?? and abs(val_def-sqrt(x)) ??

from math import sqrt

def my_sqrt(x, precision):
    assert x >= 0 and precision > 0
    a, b = 0, x+1
    while b - a > precision:
        m = (a + b) / 2
        if m**2 > x:
            b = m
        else:
            a = m
    return (a,b)

precision = 1.e-14
for x in [0, 1, 2, 3.4, 101.]:
    val_def, val_exce = my_sqrt(x, precision)
    assert val_exce-val_def <= precision and abs(val_def-sqrt(x)) <= precision

1. Écrire une fonction sqrt_one_plus_sqrt_dicho_if_greater_than_one qui

   • accepte deux arguments flottants respectivement strictement plus grand que \(1\) et strictement positifs;
   • et retourne une valeur approchée de \(\sqrt{1+\sqrt{a}}\) à \(\epsilon\) près où \(a>1\) est le premier arguments et \(\epsilon>0\) le second.

   Pour éviter les erreurs d'arrondis on ne calculera pas \(\sqrt{a}\) pour en déduire \(\sqrt{1+\sqrt{a}}\) mais on calculera directement une valeur approchée de cette dernière quantité. Pour vous aider

   • on remarque que si \(a>1\) alors \(\sqrt{1+\sqrt{a}}\) est solution de \((x^{2}-1)^{2}=a\), l'unique autre solution réelle étant \(\pm\sqrt{1+\sqrt{a}}\) (car \(a>1\));
   • on donne ci-dessous la représentation graphique de \(x\mapsto{}(x^{2}-1)^{2}\);
   • on pourra remarquer que tout \(\alpha\geq1\) vérifie \(\sqrt{\alpha}\leq\alpha\) et donc pour \(a\geq1\) on a \(\sqrt{1+\sqrt{a}}\leq1+\sqrt{a}\leq{}1+a\).

   

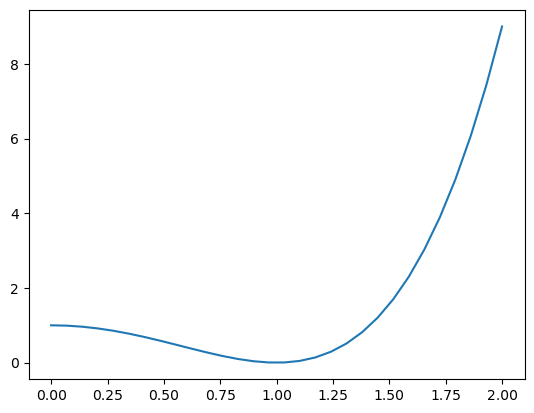
   from math import sqrt
   
   def sqrt_one_plus_sqrt_dicho_if_greater_than_one(a, precision):
       assert a > 1 and precision > 0
       g, d = 0, x+1
       while d - g > precision:
           m = (a + b) / 2
           if m**2 > x:
               b = m
           else:
               a = m
       return (a,b)
   
   precision = 1.e-14
   for x in [0, 1, 2, 3.4, 101.]:
       val_def, val_exce = my_sqrt(x, precision)
       assert val_exce-val_def <= precision and abs(val_def-sqrt(x)) <= precision
   

2. Reprendre la question precedente en supposant uniquement \(a\geq0\). On appellera la nouvelle fonction sqrt_one_plus_sqrt_dicho. On remarquera
   • qu'alors les solutions réelles à \((x^{2}-1)^{2}=a\) sont \(\pm\sqrt{1\pm\sqrt{a}}\) dès qu'elles sont définies (elles le sont touteset sont distinctes si \(0\leq{}a<1\)).
   • que tout \(\alpha\geq0\) vérifie \(\sqrt{\alpha}\leq1+\alpha\) et donc pour \(a\geq0\) on a \(\sqrt{1+\sqrt{a}}\leq1+(1+\sqrt{a})\leq2+\sqrt{a}\leq1+(2+a)\leq{}3+a\).
3. Que doit-on changer dans sqrt_one_minus_sqrt_dicho pour obtenir une fonction sqrt_one_minus_sqrt_dicho qui retourne une valeur approchée à une précison donnée de \(\sqrt{1-\sqrt{a}}\) (en supposant \(0\leq{}a\leq{}1\))? Écrire une telle fonction.