- Créer un sous-dossier «TP06» dans le dossier «TP_informatique_commune» de votre repertoire personnel
- Si on vous demande d'écrire un script python à la question 3\c) de l'activité 2 du TP 7 vous enregistrez ce script dans un fichier nommé «tp07_act02_q03c.py». Remarquez que l'on utilisera toujours deux chiffres décimaux pour représenter les entiers et que l'on va toujours du général vers le particulier car ainsi l'ordre alphabétique correspond à l'ordre tri chronologique.
- On rendra son code modulaire en utilisant systématiquement des fonctions
- On testera toutes ses fonctions
1. Introduction
Compléter la fonction suivante pour qu'elle retourne \(a^{n}\) où \(a\) est supposé de type numérique et
nest un entier naturel (on vérifiera quenest bien positif ou nul).def puiss(a, n): if n ==0: ?? return a * puiss(??, ??)- Que provoque l'appel
puiss(2, -1)? Pourquoi? - Modifier votre fonction pour qu'elle fonctionne avec
nentier de signe quelconque.
- Pour \(n\geq0\) entier on pose
\(T_{n}=\prod_{k=0}^{n}\frac{\ln{(e+k)}}{\sqrt{k}+1}\).
- Écrire une fonction itérative (c'est à dire qui utilise des
boucles)
calc_tn_iterativeacceptant un unique argumentnque l'on supposera entier positif ou nul et qui retourne \(T_{n}\). - Un étudiant ajoute le test ci-dessous.
- Vérifier que le second échoue mais pas le premier.
- Expliquer pourquoi le premier test est tout de même dangereux et ne doit pas être écrit ainsi puis réécrire ce test autrement.
- Écrire une fonction itérative (c'est à dire qui utilise des
boucles)
Compléter la fonction
calc_tn_recursivesuivante pour qu'elle retourne elle aussi \(T_{n}\).def calc_tn_recursive(n): if ??: ?? return ?? * calc_tn_recursive(??)- Écrire une fonction récursive
factorielle_recursivequi retourne la factorielle de son argument. - Écrire une fonction récursive
produit_elmts_listequi retourne le produit des éléments de la liste de valeurs numériques passée en argument. Rappel utile: siLest une liste et sia<=bsont deux indices de cette liste alorsL[a:b]désigne la sous-liste deL(en fait une copie superficielle de la sous-liste deL) constitutuée des éléments d'indiceivérifianta<=i<b.L[a:](équivalent àL[a:len(L)]mais à privilégier) désigne la sous-liste deL(en fait une copie superficielle de la sous-liste deL) constitutuée des éléments d'indiceivérifianta<=i.L[:b](équivalent àL[0:b]mais à privilégier) désigne la sous-liste deL(en fait une copie superficielle de la sous-liste deL) constitutuée des éléments d'indiceivérifianti<b.
2. Dessins recursifs
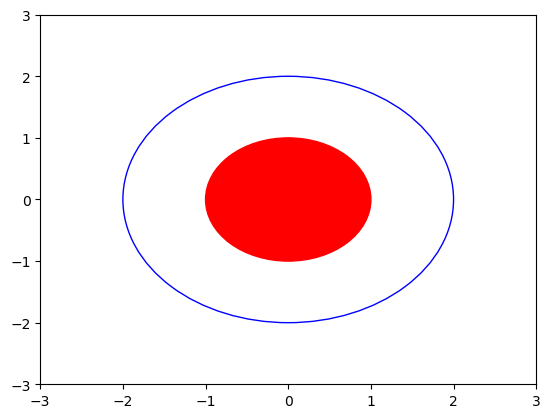
Vérifier que le code ci-dessous affiche l'image donnée encore en-dessous
import matplotlib.pyplot as plt fig, axes = plt.subplots() axes.set_xlim(-3, 3) axes.set_ylim(-3, 3) disque = plt.Circle((0, 0), 1, color="r") axes.add_artist(disque) circle = plt.Circle((0, 0), 2, fill=False, color="b") axes.add_artist(circle) plt.show()
Compléter le programme itératif ci-dessous afin qu'il affiche l'image ci-dessous où les cercles bleus sont de rayon \(1\), \(2\) et \(3\) et les petits disques sont de rayon \(0,2\). On pourra penser aux racines \(n\)-ièmes de l'unité
import matplotlib.pyplot as plt from math import pi, cos, sin fig, axes = plt.subplots() axes.set_xlim(-5, 5) axes.set_ylim(-5, 5) nbr_sat_min, nbr_sat_max = 3, 5 R_min, delta_R = 1, 1 diam_sat = 0.2 R = R_min for n in range(nbr_sat_min, nbr_sat_max+1): # boucle sur les grands cercles circle = plt.Circle((0, 0), R, color="b", fill=False) axes.add_artist(circle) for k in range(??): # boucle sur les petits disques du grand cercle theta = ?? x, y = ?? * cos(??), ?? * sin(??) disque = plt.Circle((??, ??), ??, color="r") axes.add_artist(disque) R += delta_R plt.show()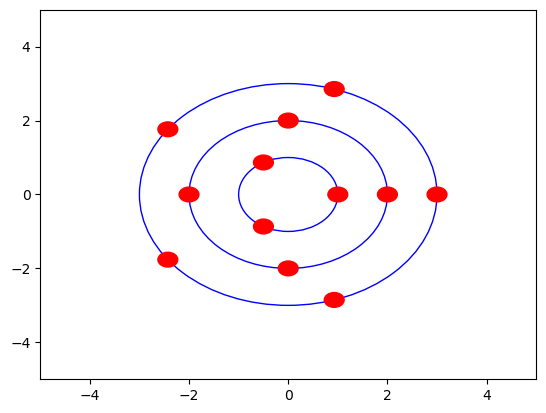
Modifier le programme récursif suivant pour qu'il affiche l'image ci-dessous (où à la taille des cinq satellites et leur distance à leur planète est chaque fois divisée par \(3\), où le diamètre de l'étoile initiale est de \(0.3\) et la distance à ses planètes de \(1\)).
import matplotlib.pyplot as plt from ?? import pi, cos fig, axes = plt.subplots() axes.set_xlim(-2, 2) axes.set_ylim(-2, 2) nbr_sat_par_planete = 5 def trace(x_centre, y_centre, profondeur, profondeur_max, diametre, dist_a_planete): ?? ??: disque = plt.Circle((x_centre, y_centre), diametre, color="r") axes.add_artist(disque) for k in range(??): theta = ?? x, y = ?? + ?? * cos(??), ?? + ?? * sin(??) trace(??, ??, ??, ??, ??, ??) trace(??, ??, ??, ??, ??, ??) plt.show()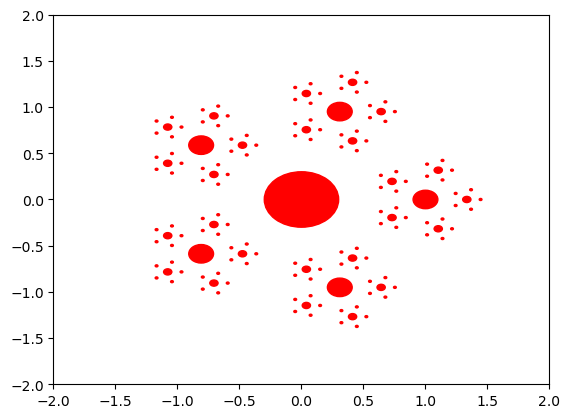
Créer un programme recursif qui affiche l'image ci-dessous. Aides:
- Le centre de gravité d'un triangle se situe aux deux-tiers de chaque médiane en partant de son sommet.
- les hauteurs d'un triangle équilatéral de côté \(a\) sont de longueur \(a\times\sqrt{3}/2\).
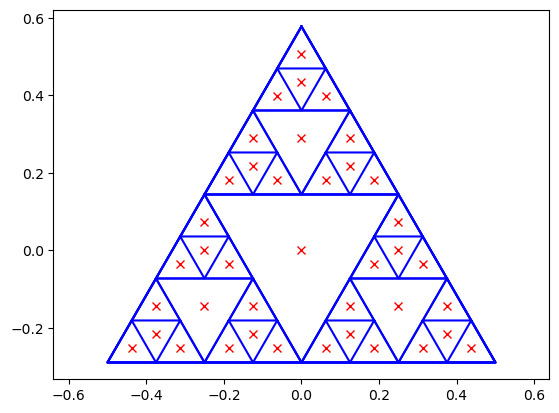
Modifier votre programme pour qu'il affiche
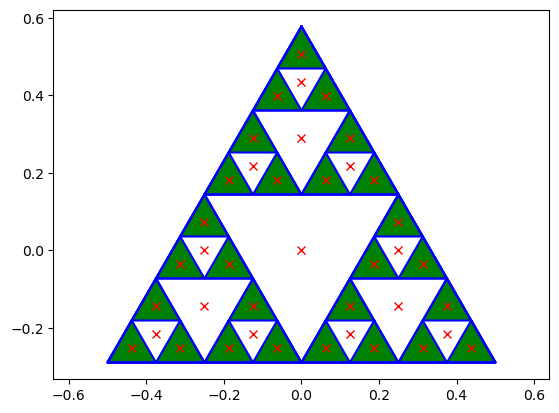
3. Applications
On souhaite écrire une fonction
perm_setadmettant un unique paramètrenet qui retourne la liste des permutation de l'intervalle d'entiers \(\iinterff{1}{n}\). Ainsi l'appelperm_set(3)doit retourner[[3, 2, 1], [3, 1, 2], [2, 3, 1], [1, 3, 2], [2, 1, 3], [1, 2, 3]]
Écrire une telle fonction récursive. Remarque: on pourra utiliser les méthodes
appendetinsertdu typelist.Vérifier que le programme suivant affiche l'image donnée ci-dessous.
import matplotlib.pyplot as plt def plot_as_image(rect_array): plt.imshow(rect_array) L = [ [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0,1,1,1,1,1,0,0,1,1,1,1,0,0,0,0,0], [0,1,0,0,0,0,1,1,0,0,0,0,1,0,0,0,0], [0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0], [0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0], [0,0,1,0,0,0,0,0,1,0,1,1,0,0,0,0,0], [0,0,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0], [0,0,0,0,1,0,1,0,0,0,0,1,1,0,0,0,0], [0,0,0,0,1,0,1,0,0,0,1,0,0,1,0,0,0], [0,0,0,0,1,0,1,0,0,0,1,0,0,1,0,0,0], [0,0,0,0,1,1,1,0,0,0,0,1,1,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]] plot_as_image(L) plt.show()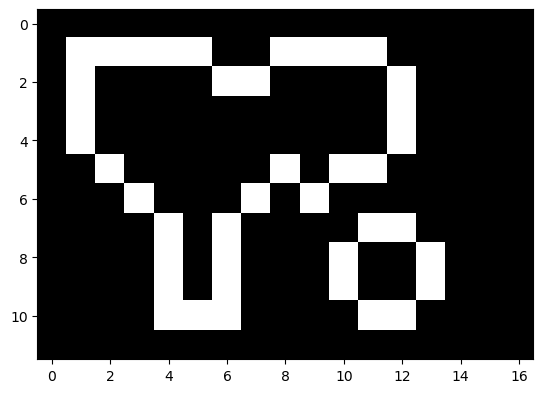
Compléter et déboguer la fonction
filldu script suivant suivante pour qu'elle remplisse de1la zone délimitée par des1et contenantL[x][y](oùxetysont les premiers arguments de la fonctionL) dans le tableauL.import matplotlib.pyplot as plt def plot_as_image(rect_array): plt.imshow(rect_array) L = [ [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0,1,1,1,1,1,0,0,1,1,1,1,0,0,0,0,0], [0,1,0,0,0,1,1,1,1,0,0,1,1,0,0,0,0], [0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0], [0,1,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0], [0,1,1,0,0,0,0,0,1,0,1,1,0,0,0,0,0], [0,0,0,1,0,0,1,1,1,1,1,0,0,0,0,0,0], [0,0,0,1,1,0,1,0,0,0,0,1,1,0,0,0,0], [0,0,0,0,1,0,1,0,0,0,1,0,0,1,0,0,0], [0,0,0,0,1,0,1,0,0,0,1,0,0,1,0,0,0], [0,0,0,0,1,1,1,0,0,0,0,1,1,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]] def fill(i, j, rect_array): if ??: ?? n = len(rect_array) p = len(rect_array[0]) ?? rect_array[i][j] = 1 delta_pos = [[1,0],[0,1],[-1,0],[0,-1]] for di, dj in delta_pos: i2, j2 = i+di, j+dj if 0 <= i2 < n and 0 <= j2 < p: fill(??, ??, ??) fill(4, 6, L) # Agit par effets de bord plot_as_image(L) plt.show()- Pouvez-vous justifier la terminaison de votre fonction
fillci-dessus?
4. Pseudo sous-chaînes
- Écrire une fonction récursive
est_sous_chaine_recacceptant deux arguments de typestret retournantTruesi le second est une sous-chaîne du premier etFalsesinon. - On dira ici qu'une chaîne
str2est une pseudo sous-chaîne de la chaînestr1si on peut obtenirstr2en supprimant des caractères àstr1.- Écrire une fonction récursive
est_pseudo_sous_chaine_iterqui renvoieTruesi si son second argument est une pseudo sous-chaîne du premier etFalsesinon.
- Écrire une fonction récursive
- Écrire une fonction récursive
est_pseudo_sous_chaine_toutes_sol_recqui fait comme précédemment mais au lieu de retrourner une slite de position possible quand il en existe les retourne toutes. Par exemple l'appelest_pseudo_sous_chaine_toutes_sol_rec("babab", "ba")doit retourner[[0, 1], [0, 3], [2, 3]].
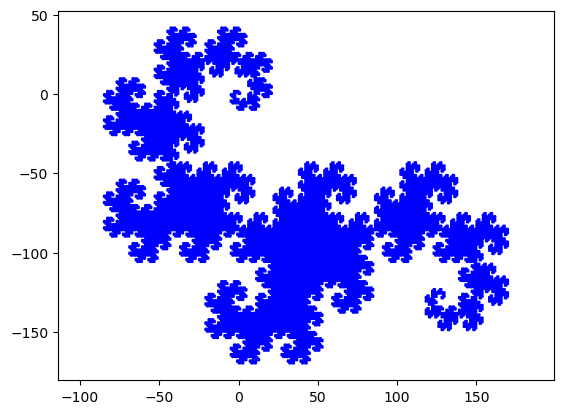
5. Dragons
Écrire une fonction qui accepte en argument une chaîne de caractères de longueur \(n\) dont les caractères sont
"X","Y","F","+"ou"-"et qui si \(r=1/n\) affiche une chaîne polygônale obtenue (remarque: à chaque instant on met à jour un point donné par ses coordonnées et une direction donnée par un vecteur)- en partant du point de coordonnées \((0,0)\) avec la direction pointée par \(\vcol{1,0}\);
- en lisant la chaîne de caractère de gauche à droite;
- en avançant de \(r\) si le caractère courant est \(F\) (pour «forward»);
- en tournant de \(90\) degrés (resp. de \(-90\) degrés) si le carctère est \(+\) (resp. \(-\));
- en ne faisant rien (si ce n'est passer au caractère suivant) si le caractère est \(X\) ou \(Y\).
Ainsi l'appel
plot_L_system("F+F-F-FF-FF+F")donne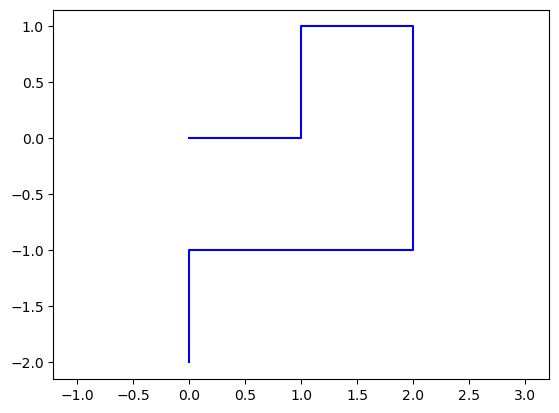
La chaîne du dragon à l'ordre \(n\) est définie ainsi
- La chaîne du dragon à l'ordre \(0\) est "FX"
- La chaîne du dragon à l'ordre \(n+1\) est définie ainsi:
- on parcourt les caractères de la chaîne du dragon à l'ordre \(n\) de la gauche vers la droite
- si on croise un
"X"on le remplace par"X+YF+" - si on croise un
"Y"on le remplace par"FX-Y" - sinon on garde le symbole tel quel.
Ainsi la chaine du dragons
- à l'ordre \(1\) est
- à l'ordre \(2\) est
Vérfier qu'après 15 itérations vous obtenez le L-système suivant