- Créer un sous-dossier «TP07» dans le dossier «TP_informatique_commune» de votre repertoire personnel
- Si on vous demande d'écrire un script python à la question 3\c) de l'activité 2 du TP 7 vous enregistrez ce script dans un fichier nommé «tp07_act02_q03c.py». Remarquez que l'on utilisera toujours deux chiffres décimaux pour représenter les entiers et que l'on va toujours du général vers le particulier car ainsi l'ordre alphabétique correspond à l'ordre tri chronologique.
- On rendra son code modulaire en utilisant systématiquement des fonctions
- On testera toutes ses fonctions
1. Rendu de monnaie
- Écrire une fonction
nbr_pièces_dictmonnaiequi accepte un dictionnaire dont les clefs sont des entiers représentant des centimes et dont les valeurs sont des entiers représentant un nombre de pièce et qui retourne le nombre total de pièces. Ainsi l'appelnbr_pièces_dictmonnaie({1: 10, 4: 2})doit retourner12. - Écrire une fonction
total_dictmonnaiequi accepte un dictionnaire dont les clefs sont des entiers représentant des centimes et dont les valeurs sont des entiers représentant un nombre de pièce et qui retourne le montant total en centimes. Ainsi l'appeltotal_dictmonnaie({1: 10, 4: 2})doit retourner18. - Écrire une fonction
total_listmonnaiequi accepte une liste de couples d'entiers dont le premier élément représente des centimes et le second un nombre de pièce et qui retourne le montant total en centimes. Ainsi l'appeltotal_listmonnaie([(1, 10), (4, 2)])doit retourner18. - Vaut-il mieux privilégier
total_dictmonnaieoutotal_listmonnaie?
- Écrire une fonction
- Écrire une fonction
meme_rendusqui accepte deux dictionnaires dont les clefs sont des entiers représentant des centimes et dont les valeurs sont des entiers représentant un nombre de pièce et qui retourneTruesi les rendus associés sont les mêmes etFalsesinon. Ainsimeme_rendus({1: 3}, {1: 3, 2: 0})doit renvoyerTrue.meme_rendus({1: 3}, {1: 4})doit renvoyerFalse.meme_rendus({1: 3}, {1: 3, 2: 1})doit renvoyerFalse.
On souhaite écrire une fonction
rendu_monnaie_illimite- qui accepte deux arguments qui sont
- un entier représentant un montant en centimes à rendre
- et une liste d'entiers triés dans l'ordre strictement
décroissant représentant les montants des pièces qui peuvent
être utilisées pour le rendu (on supposera ici que l'on
dispose d'autant de pièces de chaque type que nécessaire). À
cette question on supposera que
1fait partie de cette liste c'est à dire que l'on peut utiliser des pièces de1centimes pour le rendu de monnaie si bien que le rendu est toujours possible (quitte à n'utiliser que des pièces de 1 centimes)
- et qui retourne un dictionnaire donnant pour chaque type de pièce (représenté par sa valeur) le nombre de pièces correspondantes à rendre ou bien lève une exception.
Pour cela on utilise un algorithme dit glouton: on rend systématiquement la plus grosse pièce possible (c'est à dire inférieur à ce qu'il reste à rendre). Par exemple
rendu_monnai(6, [2, 1])doit renvoyer{2: 3}mais ni{6: 1}ni{2: 4, 1:2}.rendu_monnai(4, [3, 2])échoue car il rend d'abord3puis ne peut plus rendre la monnaie.
Écrire une telle fonction
rendu_monnaie_illimiteet vérifier qu'avec des pièces de valeurs 1, 3 et 4 l'algorithme glouton n'est pas toujours optimal en nombre de pièces utilisées pour le rendu.- qui accepte deux arguments qui sont
On souhaite écrire une fonction
rendu_monnaie- qui accepte deux arguments qui sont
- un entier représentant le montant en centimes à rendre;
- et un dictionaire d'entiers qui à chaque montant de pièce existant associe le nombre (qui peut être nul) de pièces de ce type disponibles pour le rendu;
- et qui retourne un dictionnaire donnant pour chaque type de
pièce (toujours représenté par sa valeur) le nombre de pièces
correspondantes à rendre si le rendu de monnaie est possible et
Nonesinon.
Pour cela on utilisera un algorithme récursif. Aide: pour le calcul de
rendu_monnaie(S, dict)on pourra penser à rendre une pièce de monnaie d'un montantmontant_piecepuis voir si on peut maintenant rendre la monnaie surS-montant_piece(avec une pièce de ce type en moins!)…- qui accepte deux arguments qui sont
- Écrire une fonction
rendu_monnaie_minianalogue à la précédente mais qui rend toujours la monnaie avec un nombre minimal de pièces…
2. Allocation de ressources
On dispose d'une salle de conférence qui est très demandé: beaucoup de demandes de créneaux sont faites la même journée, chacune étant représentée par un intervalle de temps \(\interfo{d_{i}}{f_{i}}\) avec \(d_{i}\lt{}f_{i}\). Malheureusement des demandes sont incompatibles c'est à dire qu'il est fort possible d'avoir \(\interfo{d_{i}}{f_{i}}\interfo{d_{j}}{f_{j}}\neq\emptyset\) même si \(i\neq{}j\). L'idée est de maximiser le nombre de conférences qui peuvent se tenir dans la journée. Pour cela on se propose d'étudier plusieurs algorithmes d'affectation (aussi appelés algorithmes d'allocations de ressources, la ressource à partager étant la salle de conférence).
Mathématiquement l'ensemble des demandes sera représenté par un ensemble \(\mathcal{D}=\set{\interfo{d_{1}}{f_{1}},\interfo{d_{2}}{f_{2}},\ldots,\interfo{d_{n}}{f_{n}}}\) qui sera en python représenté par une liste de couples de flottants (ou une liste de listes de longueur \(2\) de flottants).
Un premier algorithme glouton auquel on peut penser est le suivant: on tri les demandes par heure de début de conférence (remarquons que cet ordre n'est pas unique car des demandes peuvent être distinctes et commencer à la même heure: la relation binaire utilisée n'est pas une relation d'ordre car elle n'est pas antisymétrique) puis on parcourt les demandes dans cet ordre
- en commençant avec une liste de demandes retenues vide;
- puis
- si la demande courante n'est pas incompatible avec celles qui ont déjà été retenues alors on ajoute cette demande aux demandes retenues;
- si la demande courante est incompatible avec une demande déjà retenue (c'est à dire avec cet algorithme avec la dernière demande retenue) alors on passe à la demande suivante.
Remarquons qu'avec cet algorithme si une demande commence strictement avant toutes les autres alors elle sera nécessairement retenue (en premier). Ainsi avec les \(4\) demandes \(\interfo{0}{6}\), \(\interfo{1}{2}\), \(\interfo{3}{4}\), \(\interfo{4}{7}\) et \(\interfo{6}{7}\) représentées graphiquement ci-dessous
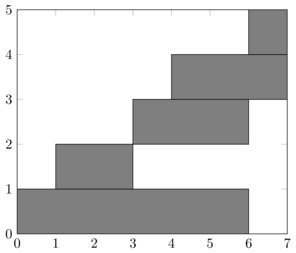
l'algorithme
- part d'une liste de demandes acceptées vide;
- y ajoute \(\interfo{0}{6}\);
- ignore dans l'ordre les demandes \(\interfo{1}{2}\), \(\interfo{3}{4}\), \(\interfo{4}{7}\) car elles sont incompatibles avec la demande acceptée \(\interfo{0}{6}\);
- puis ajoute \(\interfo{6}{7}\);
et on obtient donc l'ordonnancement suivant
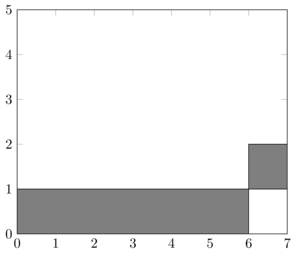
qui n'est pas optimal car il est possible de planifier \(3>2\) conférences.
Copier-coller le code ci-dessous et compléter la fonction
teste_tri_liste_demandes_par_date_debutqui doit tester la fonctiontri_liste_demandes_par_date_debut(qui doit évidemment avoir un fonctionnement conforme à sa documentation)def tri_liste_demandes_par_date_debut(L): """Fonction qui retourne une copie triée la liste de demandes L triée par heure de début. Arguments: L: liste de couples (ou de listes de longueur 2) de valeurs numériques (entiers ou flottants) Retourne: une copie de L où les demandes sont triée par heure de début """ if type(L) != tuple and type(L) != list: raise Exception("Les demandes doivent être représentées par un tuple/une liste") return sorted(L, key=lambda demande: demande[0]) def teste_tri_liste_demandes_par_date_debut(): assert ... assert ... teste_tri_liste_demandes_par_date_debut()- Écrire une fonction
deux_creneaux_sont_compatqui accepte deux couples de valeurs numériques et retourneTruesi elles sont compatibles etFalsesinon (sans hypotheses sur les dates de début ou de fin ou la longueur de ces demandes). Remarquons que deux créneaux sont compatible ssi l'un est tout entier avant ou tout entier après l'autre… - En déduire une fonction
liste_creneaux_tous_compat_avec_autre_creneauqui accepte une liste de creneaux et un creneau en arguments et qui retourneTruesi le creneau donné en argument est compatible avec tous les créneaux de la liste etFalsesinon. - Écrire une fonction
algo_glouton_min_heure_debutimplémentant l'algorithme glouton d'affectation décrit ci-dessus (on utilisera les fonctionstri_liste_demandes_par_date_debutetdeux_creneaux_sont_compat).
On change d'algorithme d'affectation pour un autre algorithme glouton: au ileu de minimiser localement (c'est à dire à chaque étape) l'heure de début des demandes retenues on choisit de minimiser localement la longueur des demandes (càd parmi les demandes qui sont compatibles avec celles déjà retenues on choisit la demande \(\interfo{d_{i}}{f_{i}}\) minimisant \(f_{i}-d_{i}\)) tant que cela est possible. Ainsi avec les demandes
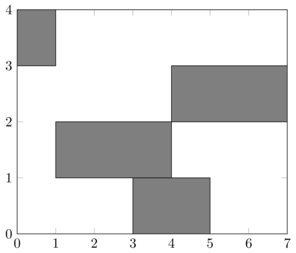
l'algorithme
- part d'une liste de demande acceptées vide;
- y ajoute \(\interfo{0}{1}\);
- y ajoute \(\interfo{3}{5}\).
et on obtient donc l'ordonnancement non optimal suivant
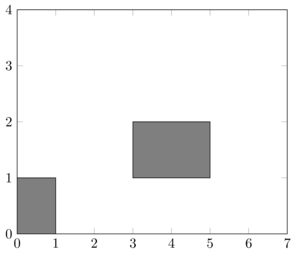
Copier-coller le code ci-dessous et compléter la fonction
teste_tri_liste_demandes_par_longueurqui doit tester la fonctiontri_liste_demandes_par_longueur(qui doit évidemment avoir un fonctionnement conforme à sa documentation)def tri_liste_demandes_par_longueur(L): """Fonction qui retourne une copie triée la liste de demandes L triée par longueurs croissantes. Arguments: L: liste de couples (ou de listes de longueur 2) de valeurs numériques (entiers ou flottants) Retourne: une copie de L où les demandes sont triée par heure de début """ if type(L) != tuple and type(L) != list: raise Exception("Les demandes doivent être représentées par un tuple/une liste") return sorted(L, key=lambda demande: demande[1]-demande[0]) def teste_tri_liste_demandes_par_longueur(): L = [[2, 4], [1, 5], [0, 6]] res = ?? assert tri_liste_demandes_par_longueur(L) == res L = [[2, 4], [1, 5], [0, 6]] res = ?? assert tri_liste_demandes_par_longueur(L) == res L, res = [], [] assert tri_liste_demandes_par_longueur(L) == res teste_tri_liste_demandes_par_longueur()- Écrire une fonction
algo_glouton_min_longueur_creneauimplémentant l'algorithme glouton d'affectation décrit ci-dessus (on utilisera les fonctionstri_liste_demandes_par_longueuretdeux_creneaux_sont_compat).
- De façon semblable, écrire maintenant un algorithme glouton
algo_glouton_min_heure_finqui minimise à chaque étape la date de fin de la conférence. Remarque importante: on peut montrer (mais ce n'est pas facile) que contrairement aux autres algorithmes gloutons ci-dessus cet algorithme glouton est toujours optimal en nombre de créneaux retenus!
3. Enveloppe convexe
Le but est d'écrire un algorithme qui accepte une liste L de
(coordonnées de) points du plan (représentés à l'aide de couples de
longueur 2) et retourne une liste de points de l'enveloppe convexe de
ces points
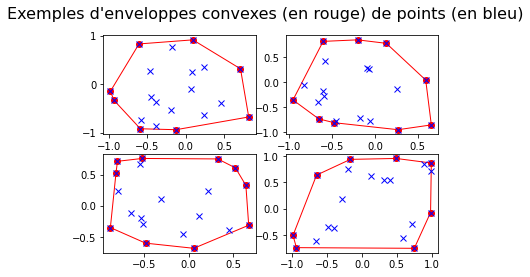
3.1. Vérification d'une enveloppe convexe
On souhaite vérifier qu'une liste de points (représentée par une liste de tuple de longueur 2) définit une enveloppe de points parcourue dans le sens trigonométrique. On admettra
- que pour deux vecteurs \(\vcolnamed{\vec{u}}{u_{x},u_{y}}\) et \(\vcolnamed{\vec{v}}{v_{x},v_{y}}\) l'angle orienté \(\angle{\vec{u}}{\vec{v}}\) et le produit en croix \(u_{x}v_{y}-u_{y}v_{x}\) vérifient \(u_{x}v_{y}-u_{y}v_{x} =\norm{\vec{u}}\norm{\vec{v}}\sin{(\angle{\vec{u}}{\vec{v}})}\). En particulier si on choisit le représentant principal de l'angle c'est à dire \(\angle{\vec{u}}{\vec{v}}\in\interof{-\pi}{\pi}\) alors le signe de ce produit en croix permet de savoir si \(\angle{\vec{u}}{\vec{v}}\in\interof{0}{\pi}\) ou \(\angle{\vec{u}}{\vec{v}}\in\interof{-\pi}{0}\).
- qu'une liste de points \((P_{1},\dots,P_{n})\) définit une enveloppe de points parcourue dans le sens trigonométrique si et seulement si pour tout \(1\leq{}i\leq{}n+1\) les points \(P_{i}\), \(P_{i+1}\) et \(P_{i+2}\) sont parcourus positivement
Écrire une fonction
ccw(pour counterclockwise: sens inverse des aiguilles d'une montre) acceptant trois tuples de longueur 2 représentant des points du plan et renvoyantTrues'ils sont dans le sens trigonométrique et false sinon. Pour tester votre fonction vous vérifierez votre résultat sur les triplets de points de la listetriplet_points_dans_sens_trigo(qui sont tous dans le sens trigo) ci-dessous et sur les triplet obtenus en permutant les deux premiers ou les deux derniers pointstriplet_points_dans_sens_trigo = [ [(0,1), (0,0), (1, 0)], [(0,2), (0,0), (1, 0)], [(0,3), (-5,-5), (2, 0)] ] print("ooo")- Écrire une fonction
is_positively_directed_convexe_hullacceptant un unique argument que l'on supposera être une liste de tuples de longueur 2 représentant des points du plan et qui retourneTruesi et seulement s'ils représentent une enveloppe convexe parcourue dans le sens trigonométrique. En utilisant le code ci-dessous
import random def random_point(): """Retourne un point au hasard et de façon uniforme parmi ceux dont les coordonnées sont comprises entre 0 et 1. Aucun argument. Retourne un tuple dez coordonées choisies indépendamment et uniformément entre 0 et 1. """ x_coord = random.random(0, 1) y_coord = random.random(0, 1) return (x_coord, y_coord)déterminer une valeur approchée de la probabilité que 4 points choisis au hasard uniformément entre 0 et 1 décrivent une enveloppe convexe parcourue dans le sens trigonométrique.
3.2. Une premiere méthode
L'idée est de construire l'enveloppe convexe parcourue dans le sens trigonométrique de façon itérative
- on commence par y mettre le pivot \(P\)
- si \(D\) est le dernier point ajouté à l'enveloppe convexe alors on ajoute le point \(Q\) de la liste de point dont l'angle \(\angle{\vec{OI}}{\vec{DQ}}\) pris dans \(\interfo{0}{2\pi}\) est minimal.
- Écrire l'algorihme correspondant
Quelle est la complexité de cette algorithme en fonction du nombre de points initiaux (c'est à dire en fonction de la taille des entrées)?
def indice_pivot(L): assert len(L) > 0 indice_pt_with_min_ord = 0 for i in range(len(L)): Q = L[i] if Q[1] < L[indice_pt_with_min_ord][1]: indice_pt_with_min_ord = i return indice_pt_with_min_ord pivot_test = [ [[[1, 2], [3, 4], [4, 3]], 0], [[[1, 2], [3, -4], [4, 3]], 1], [[[1, 2], [3, 4], [4, -3]], 2] ] for L, ind_min in pivot_test: assert indice_pivot(L) == ind_min, "Erreur pivot" def convex_hull(Linit): convex_hull = [] L = Linit.copy() P = pivot(L)
3.3. Parcourt de Graham
- Écrire une fonction
pivot_de_grahamqui accepte un unique argument à savoir notre liste de points et qui retourne un point \(P\) d'ordonnée minimale parmi ces points. Ce point sera appelé pivot dans la suite, toujours noté \(P\) et stoquée dans une variable globale (je sais, c'est mal…) de même nomP. - Écrire une fonction
coeff_dirqui accepte un tuple représentant un point \(A\) et qui retourne le coefficient directeur de la droite \((AP)\) où \(P\) est le pivot (on utilisera donc la variable globaleP). - L'algorithme de Graham pour la détermination d'une enveloppe
convexe parcourue dans le sens trigonométrique procède ainsi:
- On déterminer le pivot \(P\).
- On trie les autres points par ordre croissant du coefficient
directeur de la droite qu'ils forment avec le pivot et on met
le point \(P\) en premier. Rappel: Si
Lest notre liste de points alorsL.sort(key=coeff_dir)trie la listeLsuivant la quantité renvoyée parcoeff_dir. - puis on construit l'enveloppe convexe de façon itérative:
- \(P\) et le premier point de la liste