1. Manipulation d'images

Le module matplotlib permet de manipuler des images sous la forme de tableaux à deux dimensions (c'est à dire sous la forme de listes de listes). Pour tout ce TP on fournit les fonctions ci-dessous (à copier en haut de vos scripts) 

import matplotlib.pyplot as plt
import numpy as np

def plot_as_image(rect_array):
    """Affiche l'image correspondant au tableau rect_array"""
    plt.figure()
    plt.axis('off')
    plt.figimage(np.array(rect_array))
    plt.show()

def plot_as_gray_image(rect_array):
    """Affiche l'image correspondant au tableau rect_array"""
    plt.figure()
    plt.axis('off')
    plt.figimage(np.array(rect_array), cmap=plt.gray())
    plt.show()

def image_to_array(chemin_image):
    """Retourne un tableau correspondant à l'image de chemin d'accès
    'chemin_image'
    """
    return list(plt.imread(chemin_image))

Dans tout ce TP nous travaillerons sur des images au format png du tableau "Le Cri" (Skrik)) du peintre expressionniste norvégien Edvard Munch. Ces dernieres sont à télécharger ci-dessous en téléchargant les fichiers dans un sous-dossier nommé img du dossier de votre TP (ainsi tous les script de ce TP doivent être dans le même dossier du sous-dossier "img" qui lui-même contient les fichiers munch_le_cri.png et munch_le_cri_NB.png).

munch_le_cri.png
munch_le_cri_NB.png

Dans la suite on supposera que cette image est sauvergardée dans le dossier de ce TP (avec le même nom munch_le_cri.png). On supposera de plus que la ligne suivante est toujours présente en haut de vos scripts 

import os
img_fpath = os.path.join("img", "munch_le_cri.png")
img_NB_fpath = os.path.join("img", "munch_le_cri_NB.png")

En résumé on commencera ses scripts par 

import matplotlib.pyplot as plt
import numpy as np

def plot_as_image(rect_array):
    """Affiche l'image correspondant au tableau rect_array"""
    plt.figure()
    plt.axis('off')
    plt.figimage(np.array(rect_array))
    plt.show()

def plot_as_gray_image(rect_array):
    """Affiche l'image correspondant au tableau rect_array"""
    plt.figure()
    plt.axis('off')
    plt.figimage(np.array(rect_array), cmap=plt.gray())
    plt.show()

def image_to_array(chemin_image):
    """Retourne un tableau correspondant à l'image de chemin d'accès
    'chemin_image'
    """
    return list(plt.imread(chemin_image))

import os
img_fpath = os.path.join("img", "munch_le_cri.png")
img_NB_fpath = os.path.join("img", "munch_le_cri_NB.png")

  1. Vérifier que le programme suivant affiche une image sinon appeler le professeur (rappel: comme écrit ci-dessus vous devez enregistrer l'image nommée munch_le_cri.png dans un dossier nommé img du dossier contenant votre script) 

    import matplotlib.pyplot as plt
import numpy as np

def plot_as_image(rect_array):
    """Affiche l'image correspondant au tableau rect_array"""
    plt.figure()
    plt.axis('off')
    plt.figimage(np.array(rect_array))
    plt.show()

def plot_as_gray_image(rect_array):
    """Affiche l'image correspondant au tableau rect_array"""
    plt.figure()
    plt.axis('off')
    plt.figimage(np.array(rect_array), cmap=plt.gray())
    plt.show()

def image_to_array(chemin_image):
    """Retourne un tableau correspondant à l'image de chemin d'accès
    'chemin_image'
    """
    return list(plt.imread(chemin_image))

import os
img_fpath = os.path.join("img", "munch_le_cri.png")
img_NB_fpath = os.path.join("img", "munch_le_cri_NB.png")

# Rappel: les lignes précédentes devront toujours être ajoutées en
# début de script dans ce TP

image_as_array = image_to_array("./img/munch_le_cri.png")
plot_as_image(image_as_array)
plt.show()

    1. Vérifier que le programme suivant affiche une image (sinon appeler le professeur) 

      L = [[0, 0, 0, 0, 0],
     [0, 1, 1, 1, 1],
     [0, 1, 2, 2, 2],
     [0, 1, 2, 3, 3],
     [0, 1, 2, 3, 4]]

plot_as_gray_image(L)

    2. Vérifier que le module matplotlib effectue "une balance des blancs" automatique en vérifiant que le script ci-dessous affiche la même image que précédemment 

      L = [[0, 0, 0, 0, 0],
     [0, 1, 1, 1, 1],
     [0, 1, 2, 2, 2],
     [0, 1, 2, 3, 3],
     [0, 1, 2, 3, 4]]

# Déformation affine de l'intensité:
#   on multiplie ar 2 puis on ajoute 3 à l'intensité de chaque pixel 
L_deformation_affine = [[2*color+3 for color in line] for line in L]

plot_as_gray_image(L_deformation_affine)

    3. Une image couleur est représentée par un tableau de dimension trois (càd une liste de listes de listes représentant une liste de lignes chacune étant une liste de pixel chacun étant une liste de trois flottants compris entre \(0\) et \(1\) représentant chacun une composante primaire de la couleur du pixel) de flottants compris entre 0 et 1. À l'aide du script suivant déterminer l'ordre correct des trois canaux de couleur: est-ce RVB, RBV, BRV, BVR, RVB ou RBV? 

      L = [[[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]],
     [[0., 1., 0.], [0., 1., 0.], [0., 1., 0.]],
     [[0., 0., 1.], [0., 0., 1.], [0., 0., 1.]],
     [[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]],
     [[0., 1., 1.], [0., 1., 1.], [0., 1., 1.]],
     [[1., 0., 1.], [1., 0., 1.], [1., 0., 1.]],
     [[1., 1., 0.], [1., 1., 0.], [1., 1., 0.]]]

plot_as_image(L)
      1. Soit une image couleur représentée par un tableau L. Dans l'expression L[i][j][k] quel indice parmi i, j ou k est
        1. un indice ligne?
        2. un indice colonne?

        3. un indice de canal (=couleur)? 

          Dans ~L[i][j][k]~, ~i~ est un indice ligne, ~j~ est un indice colonne,
~k~ est un indice de canal.
      2. Si tab est un tableau de dimension \(3\) de taille \(n\times{}p\times{}3\) représentant une image couleur, dire en français à quoi correspond l'expressions suivante (on pourra écrire une phrase sur le modèle de la suivante: «cette expression correspond à la composante rouge/verte/bleue du pixel situé en … de l'image»).
        1. tab[0][0][0]?
        2. tab[-1][0][1]?
        3. tab[0][-1][2]?
        4. tab[-1][-1][-1]?
      1. ~tab[0][0][0]~: canal rouge du pixel en haut à gauche.
2. ~tab[-1][0][1]~: canal vert du pixel en bas à gauche.
3. ~tab[0][-1][2]~: canal bleu du pixel en haut à droite.
4. ~tab[-1][-1][-1]~: canal bleu du pixel en bas à droite.

  3. Compléter les fonctions symetrie_axe_vertical_v1 et symetrie_axe_vertical_v2 qui prennent en argument une image (sous la forme d'un tableau) et retourne une nouvelle image obtenue par symétrie autour d’un axe vertical passant par le milieu de l’image (donc la gauche passe à droite et réciproquement). 

    def symetrie_axe_vertical_v1(im):
    n, p = len(??), len(??)
    im_res = ??
    for i in range(??):
        im_res.append(im[??])
    return ??

    def symetrie_axe_vertical_v1(im):
    n, p = len(im), len(im[0])
    im_res = []
    for i in range(n):
        im_res.append(im[n-1-i])
    return im_res

    def symetrie_axe_vertical_v2(im):
    n, p = len(??), len(??)
    return [im[??] for i in ??] # liste définie par compréhension

    def symetrie_axe_vertical_v2(im):
    n = len(im)
    return [im[n-1-i] for i in range(n)] # liste définie par compréhension

    def symetrie_axe_vertical_v2(im):
    n = len(im)
    return [im[i] for i in range(n-1,-1,-1)]

    Ainsi chacun des scripts suivants doit afficher l'image qui lui suit (images identiques évidemment) 

    im = image_to_array(img_fpath)
im_sym = symetrie_axe_vertical_v1(im)
plot_as_image(im_sym)
    0163f062dbf410aa2a535565f0ffc37ccb7e7c63.png 
    im = image_to_array(img_fpath)
im_sym = symetrie_axe_vertical_v2(im)
plot_as_image(im_sym)
    0163f062dbf410aa2a535565f0ffc37ccb7e7c63.png

  4. Écrire une fonction symetrie_axe_horizontale qui prend en argument une image (sous la forme d'un tableau de dimension) et retourne une nouvelle image, obtenue par symétrie autour d’un axe horizontale passant par le milieu de l’image. 

    def symetrie_axe_horizontale_v1(im):
    n, p = len(im), len(im[0])
    im_res = []
    for i in range(n):
        ligne_res = []
        for j in range(p):
            ligne_res.append(im[i][p-1-j])
        im_res.append(ligne_res)
    return im_res

    def symetrie_axe_horizontale_v2(im):
    n, p = len(im), len(im[0])
    im_res = []
    for ligne_im in im:
        ligne_res = [ligne_im[p-1-i] for i in range(p)]
        im_res.append(ligne_res)
    return im_res

    Ainsi les lignes suivantes doivent afficher l'image qui suit

    f330a0bafe7d828836244f97f202bdde5507960e.png

  5. Rédiger une fonction negatif qui prend en argument une image couleur et retourne son négatif, c’est-à-dire l’image dans laquelle chaque composante de couleur c de chaque pixel est remplacée par sa valeur complémentaire 1-c. Remarque: éviter d'utiliser des indices, ici vous n'en avez pas besoin. 

    def img_negatif(im):
    n, p = len(im), len(im[0])
    im_res = []
    for ligne in im:
        ligne_res = [1-c for c in ligne]
        im_res.append(ligne_res)
    return im_res
    7a7eecd6bd8df067ef0a9c6059679c0d0d8b5b6f.png

    1. Écrire une fonction split_color_channels(imtab) qui prend en argument un tableau numpy imtab représentant une image couleur et retourne un triplet de tableaux numpy de même taille représentant dans l'ordre la couleur rouge, la couleur verte et la couleur bleue. Pour afficher les trois images côte à côte on utilisera le code suivant 

      # Créer une figure constituée de trois repères disposés en 3 colonnes
# et une ligne
fig, axes = plt.subplots(ncols=3, nrows=1)
# Afficher chaque image dans son repère
axes[0].imshow(image_rouge) # axes[0] est le repère de gauche
axes[1].imshow(image_verte) # axes[1] est le repère du milieu
axes[2].imshow(image_bleue) # axes[2] est le repère de droite

      import numpy as np
import matplotlib.pyplot as plt

im = plt.imread("./img/munch_le_cri.png")

def split_color_channels(imtab):
    res_list = [None]*3
    for color_channel in range(3):
        imres = imtab.copy()
        color_channels = [0, 1, 2]
        color_channels.remove(color_channel)
        for col in color_channels:
            imres[:,:,col] *= 0
        res_list[color_channel] = imres
    return res_list

im_list = split_color_channels(im)
fig, axes = plt.subplots(ncols=3, nrows=1)
for i in range(3):
    axes[i].imshow(im_list[i])

plt.savefig(image_filename)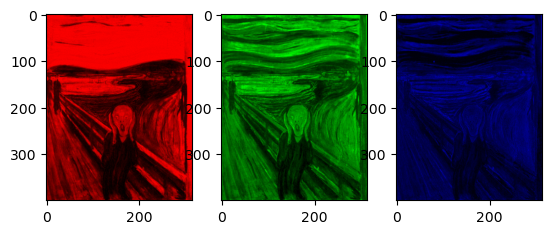
      90aff24aa604de7875615fb6d009fe38d75e3fa2.png

    1. Compléter la fonctions color_to_grayscale_simple qui accepte un tableau représentant une image couleur en argument et qui retourne un tableau représentant une image en noir et blanc (donc avec une dimension en moins) en faisant simplement la moyenne des trois composantes de couleur. 

      def color_to_grayscale_simple(im):
    n, p = len(??), len(??)
    im_res = ??
    for row in ??:
        new_row = ??
        for pixel_colors in ??:
            pix_intensity = ??
            ??.append(??)
    return ??

      import numpy as np
import matplotlib.pyplot as plt

def color_to_grayscale_simple(im):
    n, p = len(im), len(im[0])
    im_res = []
    for row in im:
        new_row = []
        for pixel_colors in row:
            pix_intensity = sum(pixel_colors)/3.
            new_row.append(pix_intensity)
        im_res.append(new_row)
    return im_res

im = plt.imread("./img/munch_le_cri.png")
im_gray = color_to_grayscale_simple(im)
plot_as_gray_image(im_gray)

    2. Compléter la fonctions color_to_grayscale qui accepte un tableau représentant une image couleur en argument et qui retourne un tableau représentant une image en noir et blanc (donc avec une dimension en moins) en utilisant la formule \(I=0.299\times{}R + 0.587\times{}G + 0.114\times{}B\) 

      def color_to_grayscale(im):
    n, p = len(??), len(??)
    im_res = ??
    for row in ??:
        new_row = ??
        for pixel_colors in ??:
            R, G, B = ??
            pix_intensity = ??
            ??.append(??)
    return ??

      import numpy as np
import matplotlib.pyplot as plt

def color_to_grayscale(im):
    n, p = len(im), len(im[0])
    im_res = []
    for row in im:
        new_row = []
        for R, G, B in row:
            pix_intensity = 0.299*R + 0.587*G + 0.114*B
            new_row.append(pix_intensity)
        im_res.append(new_row)
    return im_res

im = plt.imread("./img/munch_le_cri.png")
im_gray = color_to_grayscale(im)
plot_as_gray_image(im_gray)
      36f00f20262a9907ca131c4940e55e47c2d78d21.png

  8. (Passez plutôt à la section suivante) Rédiger une fonction appliquer_fonction(imtab, fun) qui prend en argument un tableau numpy imtab représentant une image et retourne un nouveau tableau obtenu en appliquant la fonction fun à tous les pixel de l'image imtab (chaque pixel étant donc une liste de trois flottants compris entre \(0\) et \(1\)). Vous devriez obtenir l'image ci-dessous. 

    import numpy as np
import matplotlib.pyplot as plt

im = plt.imread("./img/munch_le_cri.png")

def color_to_negative(col):
    return np.ones((1,3))-col

def appliquer_fonction(imtab, fun):
    imres = imtab.copy()
    res = np.apply_along_axis(fun, -1, imtab)
    return res

im2 = appliquer_fonction(im, color_to_negative)[:,:,0,:]
plt.imshow(im2)
plt.savefig(image_filename)
print(image_filename, end="")

    img/munch_le_cri_negative.png
    30c7305648c11d06f91e73d002f95e6b62e12019.png

2. Traitement d'images

Une première activité introductive

  1. Écrire une fonction floutage_unif_voisins_immediats qui accepte un tableau de taille notée \(n\times{}p\) représentant une image noir et blanc (pour simplifier) en argument et qui retourne un tableau représentant une image en noir et blanc de taille \((n-2)\times{}(p-2)\) représantant les pixels intérieurs (non situées au bord) dont l'intensité a été moyennée avec celle de ses \(4\) voisins directs (donc diagonale non comprise). 

    import numpy as np
import matplotlib.pyplot as plt

def floutage_unif_voisins_immediats(im):
    n, p = len(im), len(im[0])
    im_res = []
    for i in range(1, n-1):
        new_row = []
        for j in range(1, p-1):
            I = (im[i][j] +im[i-1][j]+im[i+1][j]
                 +im[i][j-1]+im[i][j+1])/5
            new_row.append(I)
        im_res.append(new_row)
    return im_res

im = plt.imread("./img/munch_le_cri_NB.png")
im_gray = floutage_unif_voisins_immediats(im)
plot_as_gray_image(im_gray)
    64757eb40a8a15c461c845a756ed4527de7baba9.png

  2. Écrire une fonction convolution_sharpen_kernel qui accepte un tableau de taille notée \(n\times{}p\) représentant une image noir et blanc (pour simplifier) en argument et qui retourne un tableau représentant une image en noir et blanc de taille \((n-2)\times{}(p-2)\) représantant les pixels intérieurs (non situées au bord) dont l'intensité \(I_{i,j}\) est remplacée par \(I'_{i,j}=5\times{}I_{i,j}-I_{i-1,j}-I_{i+1,j}-I_{i,j-1}-I_{i,j+1}\). 

    import numpy as np
import matplotlib.pyplot as plt

def convolution_sharpen_kernel(im):
    n, p = len(im), len(im[0])
    im_res = []
    for i in range(1, n-1):
        new_row = []
        for j in range(1, p-1):
            I = (5*im[i][j]-im[i-1][j]-im[i+1][j]
                 -im[i][j-1]-im[i][j+1])
            new_row.append(I)
        im_res.append(new_row)
    return im_res

im = plt.imread("./img/munch_le_cri_NB.png")
im_gray = convolution_sharpen_kernel(im)
plot_as_gray_image(im_gray)
    00cac62aeddffaa8dcd1a0f051b9680a785ac654.png

  3. Écrire une fonction convolution_ysobel_kernel qui accepte un tableau de taille notée \(n\times{}p\) représentant une image noir et blanc (pour simplifier) en argument et qui retourne un tableau représentant une image en noir et blanc de taille \((n-2)\times{}(p-2)\) représantant les pixels intérieurs (non situées au bord) dont l'intensité \(I_{i,j}\) est remplacée par \(I'_{i,j}=I_{i-1,j-1}+2*I_{i,j-1}+I_{i+1,j-1} -I_{i-1,j+1}-2*I_{i,j+1}-I_{i+1,j+1}\). 

    import numpy as np
import matplotlib.pyplot as plt

def convolution_ysobel_kernel(im):
    n, p = len(im), len(im[0])
    im_res = []
    for i in range(1, n-1):
        new_row = []
        for j in range(1, p-1):
            I = (im[i-1][j-1]+2*im[i][j-1]+im[i+1][j-1]
                 -im[i-1][j+1]-2*im[i][j+1]-im[i+1][j+1])
            new_row.append(I)
        im_res.append(new_row)
    return im_res

im = plt.imread("./img/munch_le_cri_NB.png")
im_gray = convolution_ysobel_kernel(im)
plot_as_gray_image(im_gray)
    243263f42de7b8e7858cf5797af36e6de73fe52c.png

Nous souhaitons maintenant généraliser tous les traitements précédents et traiter nos images en leur appliquant des masques linéaires c'est à dire en remplaçant la valeur de chaque pixel par une combinaison linéaire de la valeur des pixels qui lui sont adjacents.

Dans un premier temps Tous nos masques seront de taille \(3x3\) et seront donc représentés par une matrice de taille \(3x3\) comme ci-contre \(C = \begin{pmatrix} c_{11}&c_{12}&c_{13} \\ c_{21}&c_{22}&c_{23} \\ c_{31}&c_{32}&c_{33} \end{pmatrix}\). Pour expliquer l'utilisation du masque écrivons le masque C ainsi qu'un voisinage d'un pixel im[i][j] donné côte à côte

\begin{align*} C &= \begin{pmatrix} c_{11}&c_{12}&c_{13} \\ c_{21}&c_{22}&c_{23} \\ c_{31}&c_{32}&c_{33} \end{pmatrix};& M &= \begin{pmatrix} &\vdots&\vdots&\vdots& \\ \cdots&M_{(i-1);(j-1)}&M_{(i-1);(j)}&M_{(i-1);(j+1)}&\cdots \\ \cdots&M_{(i);(j-1)}&M_{(i);(j)}&M_{(i);(j+1)}&\cdots \\ \cdots&M_{(i+1);(j-1)}&M_{(i+1);(j)}&M_{(i+1);(j+1)}&\cdots \\ &\vdots&\vdots&\vdots& \\ \end{pmatrix};& \end{align*}

Si une image est représentée par la matrice \(M=(m_{ij})\) alors l'image \(M\oplus{}C=(m'_{ij})\) après avoir appliqué le masque de matrice \(C\) est (remarquer que ce n'est pas une multiplication matricielle)

\begin{equation*} m'_{ij} = \left\{\begin{array}{cccccccc} &c_{11}m_{(i-1);(j-1)}&&+&c_{12}m_{(i-1);j}&+&c_{13}m_{(i-1);(j+1)}\\ &+&c_{21}m_{i;(j-1)} &+&c_{22}m_{i;j} &+&c_{23}m_{i;(j+1)} \\ &+&c_{31}m_{(i+1);(j-1)}&+&c_{32}m_{(i+1);j}&+&c_{33}m_{(i+1);(j+1)} \end{array}\right. \end{equation*}

Pour gagner du temps nous choisirons de ne pas appliquer le masque aux pixels qui sont sur le bord de l'image.

  1. Quelle opération effectue la convolution de masque \(C= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}\)? 

    - Chaque pixel prend la valeur du pixel qui était situé par rapport à
  lui en haut à gauche: cela revient à décaler l'image en bas à droite;
- mais comme pur simplifier on perd deux lignes et deux colonnes en
  fait cela revient ici à supprimer les deux dernières lignes et les
  deux dernières colonnes!

    1. Écrire une fonction applique_masque_3x3(imtab, masque) qui prend en argument une image imtab de taille \(n\times{}p\) et un masque masque de taille \(3x3\) w et qui retourne l'image de taille \((n-2)\times{}(p-2)\) après l'application du masque. Vérifier qu'avec le masque \(\begin{pmatrix}[[-1, 0,-1],[ 0, 5, 0],[-1, 0, -1]]\end{pmatrix}\) vous obtenez l'image qui suit 

      import os
import matplotlib.pyplot as plt

def applique_masque_3x3(imtab, masque):
    n, p = len(imtab), len(imtab[0])
    q = len(masque)
    assert q == 3 and len(masque[0])==3
    im_res = []
    for i in range(1,(n-1)-1):
        new_row = []
        for j in range(1,(p-1)-1):
            new_pix = (
                imtab[i-1][j-1]*masque[1-1][1-1]+imtab[i-1][j]*masque[1-1][1-1]+imtab[i-1][j+1]*masque[1-1][1+1]+
                imtab[i][j-1]*masque[1][1-1]+imtab[i][j]*masque[1][1]+imtab[i][j+1]*masque[1][1+1]+
                imtab[i+1][j-1]*masque[1+1][1-1]+imtab[i+1][j]*masque[1+1][1-1]+imtab[i+1][j+1]*masque[1+1][1+1]
            )
            new_row.append(new_pix)
        im_res.append(new_row)
    return im_res          

      masque = [ [-1, 0,-1],
           [ 0, 5, 0],
           [-1, 0, -1]]

im = image_to_array(img_NB_fpath)
im_traitee = applique_masque_3x3(im, masque)
plot_as_gray_image(im_traitee)
      0b4d39f14d285fef59c53f91deaaa789e7fcd3de.png

    2. Appliquer les masques de taille \(3\times{}3\) appelés ridge detection de cette page wikipedia à l'image en noir et blanc du cri de Munch. 

      masque_rd1 = [[-1, -1, -1],
              [-1,  8, -1],
              [-1, -1, -1]]

im = image_to_array(img_NB_fpath)
im_traitee = applique_masque_3x3(im, masque)
plot_as_gray_image(im_traitee)
      0b4d39f14d285fef59c53f91deaaa789e7fcd3de.png 
      masque_rd1 = [[ 0, -1,  0],
              [-1,  4, -1],
              [ 0, -1,  0]]

im = image_to_array(img_NB_fpath)
im_traitee = applique_masque_3x3(im, masque)
plot_as_gray_image(im_traitee)
      0b4d39f14d285fef59c53f91deaaa789e7fcd3de.png

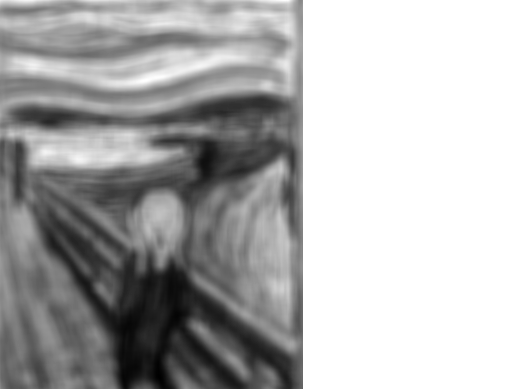
  3. Écrire une fonction applique_masque(imtab, masque) qui prend en argument une image imtab de taille \(n\times{}p\) et un masque masque de taille \(qxq\) où \(q=2k+1\) est impair et qui retourne l'image de taille \((n-k)\times{}(p-k)\) (pour éviter les problèmes aux bords…) après l'application du masque. On vérifiera que pour les masques [ [1/q**2]*q ]*q pour q=11 et q=21 on obtient 

    import os
import matplotlib.pyplot as plt

def newpix_after_conv(imtab, masque, i, j):
    q = len(masque)
    assert q % 2 == 1
    k = q // 2
    newpix = 0
    for i_m in range(q):
        for j_m in range(q):
            newpix += imtab[i+k-i_m][j+k-j_m]*masque[i_m][j_m]
    return newpix

def applique_masque_qxq(imtab, masque):
    n, p = len(imtab), len(imtab[0])
    q = len(masque)
    assert q == len(masque[0])  # masque supposé carré
    assert q % 2 == 1
    k = q // 2 # q = 2k+1
    im_res = []
    for i in range(k,(n-1)-k):
        new_row = []
        for j in range(k,(p-1)-k):
            new_pix = newpix_after_conv(imtab, masque, i, j)
            new_row.append(new_pix)
        im_res.append(new_row)
    return im_res

    q = 5
masque = [ [1/q**2]*q ]*q
im = image_to_array(img_NB_fpath)
im_traitee = applique_masque_qxq(im, masque)
plot_as_gray_image(im_traitee)
    804cb1d7c980fc6a86d7a72ce4f762d200fd2860.png 
    q = 11
masque = [ [1/q**2]*q ]*q
im = image_to_array(img_NB_fpath)
im_traitee = applique_masque_qxq(im, masque)
plot_as_gray_image(im_traitee)
    0b742fb9fe82680dc0bf3bea2347911906ce0ea4.png

3. Redimensionnement d'images

Ici on utilisera cette photo du chateau de saint Fargeaux que l'on enregistrera encore dans un dossier img du dossier courant. 

import  os
img_st_farg_small_fpath = os.path.join("img", "saint_fargeaux_NB_small.png")
img_st_farg_small = image_to_array(img_st_farg_small_fpath)
plot_as_gray_image(img_st_farg_small)
ccac152fdb6ca631642572f960843efbc3c91832.png

  1. Vérifier que le code ci-dessous affiche bien l'image qui lui suit 

    import  os
img_st_farg_small_fpath = os.path.join("img", "saint_fargeaux_NB_small.png")
img_st_farg_small = image_to_array(img_st_farg_small_fpath)
plot_as_gray_image(img_st_farg_small)
    ccac152fdb6ca631642572f960843efbc3c91832.png

  2. À cette question on souhaite redimensionner horizontalement une image à un nombre donné de pixels (la dimension verticale ne changeant pas pour simplifier). Pour cela

    • pour chaque pixel \(P_{a}\) de l'image agrandie on détermine les coordonnées d'un pixel \(P_{f}\) correspondant fictif car à coordonnées flottantes dans l'image de départ. Ainsi par exemple
      • au pixel de coordonnées \((i,q)\) correspond celui de coordonnées \((i,p)\).
      • si \(q=2r\) est pair alors au pixel de coordonnées \((n,r)\) correspond celui de coordonnées \((n,p/2)\) qui ne sont plus entières en général.
    • on détermine une valeur naturel pour la couleur de \(P_{f}\) (par exemple couleur d'un pixel vrai càd à coordonnées entière le plus près ou autre)
    • on affecte la couleur choisie pour \(P_{f}\) à \(P_{a}\).

    On propose dans les questions qui suivent deux choix d'intensité pour le pixel fictif: dans un premier temps on lui affecte l'intensité du pixel le plus proche à sa gauche ou à sa droite puis dans un second temps on lui affecte une combinaison linéaire des intensités de ces deux pixels suivant leur distance à ces deux pixels adjacents.

  3. Ici on choisit d'affecter l'intensité du pixel le plus près à gauche ou à droite (nearest neighbour).

    1. Compléter le code suivant 

      from math import floor

def pixel_iind_jfrac_plus_pres(imtab, iind, jfrac):
    """Retourne le pixel situé à la ligne d'indice iind et à la colonne
    située au plus près de la colonne de position fractionnaire
    0<=jfrac<=1 (jfrac=0 pour la 1ere colonne et jfrac=1 pour la
    dernière)

    imtab: tableau à 2 dimensions représentant une image N&B.
    iind: indice ligne valide de imtab.
    jfrac: position fractionnaire de la colonne où 0<=jfrac<=1
    """
    n, p = ??
    i_res = iind
    # (j_virt=0 ssi jfrac=0) et (j_virt=p-1 ssi jfrac=1)
    j_virt = jfrac * (p-1) 
    j_g = floor(j_virt)
    j_d = j_g + 1
    if j_d > p - 1:
        assert j_g == p-1
        return ??
    pix_g, pix_d =  imtab[i_res][j_g], imtab[i_res][j_d]
    if j_virt - j_g > ??:
        return ??
    return ??

def test_pixel_iind_jfrac_plus_pres():
    imtab = [[1, 2, 4],
             [0, 3, 7]]
    iind, jfrac = 0, 0.4
    res = ??
    assert pixel_iind_jfrac_plus_pres(imtab, iind, jfrac) == res
    imtab = [[1,  2,   4],
             [0, 10, 400]]
    iind, jfrac = 1, 0.2
    res = ??
    assert pixel_iind_jfrac_plus_pres(imtab, iind, jfrac) == res

test_pixel_iind_jfrac_plus_pres()

      from math import floor

def pixel_iind_jfrac_plus_pres(imtab, iind, jfrac):
    """Retourne le pixel situé à la ligne d'indice iind et à la colonne
    située au plus près de la colonne de position fractionnaire
    0<=jfrac<=1 (jfrac=0 pour la 1ere colonne et jfrac=1 pour la
    dernière)

    imtab: tableau à 2 dimensions représentant une image N&B.
    iind: indice ligne valide de imtab.
    jfrac: position fractionnaire de la colonne où 0<=jfrac<=1
    """
    n, p = len(imtab), len(imtab[0])
    i_res = iind
    # (j_virt=0 ssi jfrac=0) et (j_virt=p-1 ssi jfrac=1)
    j_virt = jfrac * (p-1) 
    j_g = floor(j_virt)
    j_d = j_g + 1
    if j_d > p - 1:
        assert j_g == p-1
        return imtab[i_res][j_g]
    pix_g, pix_d =  imtab[i_res][j_g], imtab[i_res][j_d]
    if j_virt - j_g > 0.5:
        return imtab[i_res][j_d]
    return imtab[i_res][j_g]

def test_pixel_iind_jfrac_plus_pres():
    imtab = [[1, 2, 4], [0, 3, 7]]
    iind, jfrac = 0, 0.4
    res = 2
    assert pixel_iind_jfrac_plus_pres(imtab, iind, jfrac) == res
    imtab = [[1, 2, 4], [0, 10, 400]]
    iind, jfrac = 1, 0.2
    res = 0
    assert pixel_iind_jfrac_plus_pres(imtab, iind, jfrac) == res

test_pixel_iind_jfrac_plus_pres()

    2. Compléter le code suivant puis vérifier les résultat des deux blocs de code suivants (agrandissement d'une petite image et rétrécissement d'une grande) 

      import  os
from math import floor

def resize_image_plus_pres(imtab, new_p):
    n = len(imtab)
    new_n = n
    imtab_resized = np.zeros((n, new_p))
    for i in range(??):
        for j in range(??):
            jfrac = ?? / (??-1)
            new_pix = pixel_iind_jfrac_plus_pres(??, ??, ??)
            imtab_resized[??][??] = ??
    return ??        

      import  os
from math import floor

def resize_image_plus_pres(imtab, new_p):
    n = len(imtab)
    new_n = n
    imtab_resized = np.zeros((n, new_p))
    for i in range(new_n):
        for j in range(new_p):
            jfrac = j / (new_p-1)
            new_pix = pixel_iind_jfrac_plus_pres(imtab, i, jfrac)
            imtab_resized[i][j] = new_pix
    return imtab_resized

img_st_farg_small_fpath = os.path.join("img", "saint_fargeaux_NB_small.png")
img_st_farg_small = image_to_array(img_st_farg_small_fpath)
img_st_farg_small_reszd = resize_image_plus_pres(img_st_farg_small, 400)
plot_as_gray_image(img_st_farg_small_reszd)
6c3c538024d8a59276c1653c5beef80e5901df87.png 
img_st_farg_big_fpath = os.path.join("img", "saint_fargeaux_NB_big.png")
img_st_farg_big = image_to_array(img_st_farg_big_fpath)
img_st_farg_big_reszd = resize_image_plus_pres(img_st_farg_big, 100)
plot_as_gray_image(img_st_farg_big_reszd)
55c653ac1616c6e5a4a0b5d2a13448a3b36d1751.png
  1. Ici on choisit d'affecter d'effectuer une interpolation affine des intensités des deux pixels adjacents (situés à gauche et à droite)

    1. Compléter le code suivant 

      from math import floor

def pixel_iind_jfrac_lin_interp(imtab, iind, jfrac):
    """Retourne le pixel situé à la ligne d'indice iind et à la colonne
    située au plus près de la colonne de position fractionnaire
    0<=jfrac<=1 (jfrac=0 pour la 1ere colonne et jfrac=1 pour la
    dernière)

    imtab: tableau à 2 dimensions représentant une image N&B.
    iind: indice ligne valide de imtab.
    jfrac: position fractionnaire de la colonne où 0<=jfrac<=1
    """
    n, p = ??
    i_res = iind
    # (j_virt=0 ssi jfrac=0) et (j_virt=p-1 ssi jfrac=1)
    j_virt = jfrac * (p-1) 
    j_g = floor(j_virt)
    j_d = j_g + 1
    if j_d > p - 1:
        assert j_g == p-1
        return ??
    pix_g, pix_d =  imtab[i_res][j_g], imtab[i_res][j_d]
    pds_pix_d = j_virt - j_g
    pds_pix_g = 1 - pds_pix_d
    return ?? * pix_g + ?? * pix_d

def aprx_eq(float1, float2):
    return abs(float1-float2) < 1.e-10

def test_aprx_eq():
    assert aprx_eq(1, 1+1.e-11)
    assert aprx_eq(1+1.e-11, 1)
    assert aprx_eq(1, 1-1.e-11)
    assert aprx_eq(1-1.e-11, 1)
    assert not aprx_eq(1, 1+1.e-9)
    assert not aprx_eq(1+1.e-9, 1)
    assert not aprx_eq(1, 1-1.e-9)
    assert not aprx_eq(1-1.e-9, 1)

test_aprx_eq()

def test_pixel_iind_jfrac_lin_interp():
    imtab = [[1, 2, 4], [0, 3, 7]]
    iind, jfrac = 0, 0.25
    res = ??
    assert aprx_eq(pixel_iind_jfrac_lin_interp(imtab, iind, jfrac), res)
    imtab = [[1, 2, 4], [0, 10, 400]]
    iind, jfrac = 1, 0.75
    res = ??
    assert aprx_eq(pixel_iind_jfrac_lin_interp(imtab, iind, jfrac), res)

test_pixel_iind_jfrac_lin_interp()

      from math import floor

def pixel_iind_jfrac_lin_interp(imtab, iind, jfrac):
    """Retourne le pixel situé à la ligne d'indice iind et à la colonne
    située au plus près de la colonne de position fractionnaire
    0<=jfrac<=1 (jfrac=0 pour la 1ere colonne et jfrac=1 pour la
    dernière)

    imtab: tableau à 2 dimensions représentant une image N&B.
    iind: indice ligne valide de imtab.
    jfrac: position fractionnaire de la colonne où 0<=jfrac<=1
    """
    n, p = len(imtab), len(imtab[0])
    i_res = iind
    # (j_virt=0 ssi jfrac=0) et (j_virt=p-1 ssi jfrac=1)
    j_virt = jfrac * (p-1) 
    j_g = floor(j_virt)
    j_d = j_g + 1
    if j_d > p - 1:
        assert j_g == p-1
        return imtab[i_res][j_g]
    pix_g, pix_d =  imtab[i_res][j_g], imtab[i_res][j_d]
    pds_pix_d = j_virt - j_g
    pds_pix_g = 1 - pds_pix_d
    return pds_pix_g * pix_g + pds_pix_d * pix_d

def aprx_eq(float1, float2):
    return abs(float1-float2) < 1.e-10

def test_aprx_eq():
    assert aprx_eq(1, 1+1.e-11)
    assert aprx_eq(1+1.e-11, 1)
    assert aprx_eq(1, 1-1.e-11)
    assert aprx_eq(1-1.e-11, 1)
    assert not aprx_eq(1, 1+1.e-9)
    assert not aprx_eq(1+1.e-9, 1)
    assert not aprx_eq(1, 1-1.e-9)
    assert not aprx_eq(1-1.e-9, 1)

test_aprx_eq()

def test_pixel_iind_jfrac_lin_interp():
    imtab = [[1, 2, 4], [0, 3, 7]]
    iind, jfrac = 0, 0.25
    res = 1.5
    assert aprx_eq(pixel_iind_jfrac_lin_interp(imtab, iind, jfrac), res)
    imtab = [[1, 2, 4], [0, 10, 400]]
    iind, jfrac = 1, 0.75
    res = 205
    assert aprx_eq(pixel_iind_jfrac_lin_interp(imtab, iind, jfrac), res)

test_pixel_iind_jfrac_lin_interp()

    2. Compléter le code suivant puis vérifier les résultat des deux blocs de code suivants (agrandissement d'une petite image et rétrécissement d'une grande) 

      import  os
from math import floor

def resize_image_lin_interp(imtab, new_p):
    n = len(imtab)
    new_n = n
    imtab_resized = np.zeros((n, new_p))
    for i in range(??):
        for j in range(??):
            jfrac = ?? / (??-1)
            new_pix = pixel_iind_jfrac_lin_interp(??, ??, ??)
            imtab_resized[??][??] = ??
    return ??        

      import  os
from math import floor

def resize_image_lin_interp(imtab, new_p):
    n = len(imtab)
    new_n = n
    imtab_resized = np.zeros((n, new_p))
    for i in range(new_n):
        for j in range(new_p):
            jfrac = j / (new_p-1)
            new_pix = pixel_iind_jfrac_lin_interp(imtab, i, jfrac)
            imtab_resized[i][j] = new_pix
    return imtab_resized

      img_st_farg_small_fpath = os.path.join("img", "saint_fargeaux_NB_small.png")
img_st_farg_small = image_to_array(img_st_farg_small_fpath)
img_st_farg_small_reszd = resize_image_lin_interp(img_st_farg_small, 400)
plot_as_gray_image(img_st_farg_small_reszd)
      8d35c8e6f2447745040ca7cf4cb66aaa07824df5.png 
      img_st_farg_big_fpath = os.path.join("img", "saint_fargeaux_NB_big.png")
img_st_farg_big = image_to_array(img_st_farg_big_fpath)
img_st_farg_big_reszd = resize_image_lin_interp(img_st_farg_big, 100)
plot_as_gray_image(img_st_farg_big_reszd)
      de8405fd9dad8525c3f77d19e5db282aa25e009d.png

Auteur: Aurélien Bosché

Created: 2023-12-08 Fri 20:07

Validate