‎

Créer un sous-dossier «TP09» dans le dossier «TP_informatique_commune» de votre repertoire personnel
Si on vous demande d'écrire un script python à la question 3\c) de l'activité 2 du TP 7 vous enregistrez ce script dans un fichier nommé «tp07_act02_q03c.py». Remarquez que l'on utilisera toujours deux chiffres décimaux pour représenter les entiers et que l'on va toujours du général vers le particulier car ainsi l'ordre alphabétique correspond à l'ordre tri chronologique.
- On rendra son code modulaire en utilisant systématiquement des fonctions
- On testera toutes ses fonctions

Dans tout ce TP on triera des listes de couples (age, nom) où age est de type numérique (int ou float) et nom de type str. Remarquons que si l'on trie par exemple ces listes par âge alors il y a plusieurs possibilités pour trier une telle liste: par exemple les listes [(17,"B"),(17,"C"),(19,"D")] et [(17,"C"),(17,"B"),(19,"D")] sont toutes les deux triées par âge.

Pour les tests on pourra utiliser la liste ci-dessous

liste_a_trier = [
    (17,"L"), (15,"K"), (16,"J"),
    (14,"I"), (13,"G"), (12,"G"),
    (10,"F"), (11,"E"), (8,"D"),
    (5,"C"), (6,"B"), (7,"A")
]

1. Préléminaires

Écrire une fonction comp_large_par_age (resp. comp_stricte_par_age) qui accepte deux éléments que l'on supposera être des couples (de type tuple ou list) formés d'une valeur numérique (appelé âge) et d'une valeur de type chaîne de caractères (appelé nom) et qui retourne True si le premier est d'âge inférieur ou égal (resp. d'âge inférieur strict) au second et False sinon.

def comp_large_par_age(pers_g, pers_d):
   return pers_g[0] <= pers_d[0]

def teste_comp_large_par_age():
   pers_g, pers_d = (1, "b"), (2, "c")
   assert comp_large_par_age(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "c")
   assert not comp_large_par_age(pers_g, pers_d)
   pers_g, pers_d = (1, "b"), (2, "a")
   assert comp_large_par_age(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "a")
   assert not comp_large_par_age(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (2, "a")
   assert comp_large_par_age(pers_g, pers_d)

teste_comp_large_par_age()

def comp_stricte_par_age(pers_g, pers_d):
   return pers_g[0] < pers_d[0]

def teste_comp_stricte_par_age():
   pers_g, pers_d = (1, "b"), (2, "c")
   assert comp_stricte_par_age(pers_g, pers_d)
   pers_g, pers_d = (1, "b"), (1, "c")
   assert not comp_stricte_par_age(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "c")
   assert not comp_stricte_par_age(pers_g, pers_d)
   pers_g, pers_d = (1, "b"), (2, "a")
   assert comp_stricte_par_age(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "a")
   assert not comp_stricte_par_age(pers_g, pers_d)

teste_comp_stricte_par_age()

Écrire des fonctions similaires comp_large_par_nom et comp_stricte_par_nom qui compare cette fois par ordre lexicographique des noms (deuxième élément du tuple).

def comp_large_par_nom(pers_g, pers_d):
   return pers_g[1] <= pers_d[1]

def teste_comp_large_par_nom():
   pers_g, pers_d = (1, "b"), (2, "c")
   assert comp_large_par_nom(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "b")
   assert comp_large_par_nom(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "c")
   assert comp_large_par_nom(pers_g, pers_d)
   pers_g, pers_d = (1, "b"), (2, "a")
   assert not comp_large_par_nom(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "a")
   assert not comp_large_par_nom(pers_g, pers_d)

teste_comp_large_par_nom()

def comp_stricte_par_nom(pers_g, pers_d):
   return pers_g[1] < pers_d[1]

def teste_comp_stricte_par_nom():
   pers_g, pers_d = (1, "b"), (2, "c")
   assert comp_stricte_par_nom(pers_g, pers_d)
   pers_g, pers_d = (1, "b"), (2, "b")
   assert not comp_stricte_par_nom(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "b")
   assert not comp_stricte_par_nom(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "c")
   assert comp_stricte_par_nom(pers_g, pers_d)
   pers_g, pers_d = (1, "b"), (2, "a")
   assert not comp_stricte_par_nom(pers_g, pers_d)
   pers_g, pers_d = (2, "b"), (1, "a")
   assert not comp_stricte_par_nom(pers_g, pers_d)

teste_comp_stricte_par_nom()

Écrire une fonction liste_est_triee qui accepte deux arguments qui sont
- une liste L d'éléments de types homogènes;
- une fonction de compariason compare qui accepte deux élements supposés du type des éléments formant la liste L et qui retourne True ou False suivant que le premier est considérée inférieur ou égal au second ou non.
et qui retourne True si la liste L est triée et False sinon. Ainsi par exemple avec L=[(1,"B"), (2,"A"), (2,"C"), (4,"D")]
- l'appel liste_est_triee(L, comp_large_par_age) doit renvoyer True;
- l'appel liste_est_triee(L, comp_stricte_par_age) doit renvoyer False;
- l'appel liste_est_triee(L, comp_large_par_nom) doit renvoyer False;
```
def liste_est_triee(L, compare):
   # "L[:i] est triée" est un invrt de bcle
   for i in range(len(L)-1):
       if not compare(L[i], L[i+1]):
          return False
   return True

def teste_liste_est_triee():
   L = [(1,"B"), (2,"A"), (2,"C"), (4,"D")]
   assert liste_est_triee(L, comp_large_par_age)
   assert not liste_est_triee(L, comp_stricte_par_age)
   assert not liste_est_triee(L, comp_stricte_par_nom)
   assert not liste_est_triee(L, comp_large_par_nom)

teste_liste_est_triee()
```
On testera cette fonction avec comme second arguments comp_large_par_age et comp_large_par_nom.

2. Tri par selection

C'est un tri naturel mais il n'est pas très performant car quadratique mais est en place. Pour trier une liste L

on cherche son plus petit élément que l'on place en premiere position (par un échange);
on cherche son second plus petit élément (plus petit élément de L[1:]) que l'on place en seconde position (par un échange);
et ainsi de suite..

Compléter les fonctions tri_par_selection_en_place_v1 et tri_par_selection_en_place_v2 pour qu'elles implémentent chacune une variation de l'algorithme de tri par selection (où les variations entre les deux version concernent uniquement la façon de placer le plus petit élément).

def tri_par_selection_en_place_v1(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
   for i in ??:
       for j in ??:
           if ??:
               ??, ?? = ??, ??

def teste_tri_par_selection_en_place_v1():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_selection_en_place_v1(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_selection_en_place_v1(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_selection_en_place_v1()

def tri_par_selection_en_place_v2(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
   for i in ??:
      ind_min = i
      for j in ??:
         if ??:
            ind_min = ??
      ??, ?? = ??, ??

def teste_tri_par_selection_en_place_v2():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_selection_en_place_v2(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_selection_en_place_v2(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_selection_en_place_v2()

def tri_par_selection_en_place_v2(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
   for i in ??:
      ind_min = i
      for j in ??:
         if ??:
            ind_min = ??
      ??, ?? = ??, ??
      tab[i], tab[ind_min] = tab[ind_min], tab[i]

def teste_tri_par_selection_en_place_v2():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_selection_en_place_v2(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_selection_en_place_v2(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_selection_en_place_v2()

def tri_par_selection_en_place_v1(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
   for i in range(len(tab)):
       for j in range(i+1, len(tab)):
           if fonction_de_comparaison(tab[j], tab[i]):
               tab[j], tab[i] = tab[i], tab[j]

def teste_tri_par_selection_en_place_v1():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_selection_en_place_v1(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_selection_en_place_v1(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_selection_en_place_v1()

def tri_par_selection_en_place_v2(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
   for i in range(len(tab)):
      ind_min = i
      for j in range(i+1, len(tab)):
         if fonction_de_comparaison(tab[j], tab[ind_min]):
            ind_min = j
      tab[i], tab[ind_min] = tab[ind_min], tab[i]

def teste_tri_par_selection_en_place_v2():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_selection_en_place_v2(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_selection_en_place_v2(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_selection_en_place_v2()

3. Tri par insertion

C'est aussi un tri naturel mais il n'est pas très performant car quadratique. Pour trier une liste L

on parcourt les indices i de la liste de la gauche (premier indice exclue càd à partir de 1) vers la droite;
on fait en sorte en fin de chaque itération que L[:i+1] soit triée en insérant L[i] au bonne endroit dans la liste triée L[0:i] ce qui peut nécessiter de décaler des éléments

Écrire une fonction tri_par_selection qui accepte un argument de type liste de couples où le premier est de type numérique et qui retourne cette liste triée en place par l'algorithme de tri par selection.

def tri_par_insertion_en_place(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
    for i in ??:
        j = i - 1
        while ??:
            ??, ?? = ??, ??
            ??

def teste_tri_par_insertion_en_place():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_insertion_en_place(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_insertion_en_place(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_insertion_en_place()

def tri_par_insertion_en_place(tab, fonction_de_comparaison):
   # "L[:i] est triée" est un invrt de bcle
    for i in range(1, len(tab)):
        j = i -1
        while j >= 0 and not fonction_de_comparaison(tab[j], tab[j+1]):
            tab[j], tab[j+1] = tab[j+1], tab[j]
            j -= 1

def teste_tri_par_insertion_en_place():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   L_tri_par_age = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   tri_par_insertion_en_place(L, comp_large_par_age)
   assert L == L_tri_par_age
   L_tri_par_nom = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   tri_par_insertion_en_place(L, comp_large_par_nom)
   assert L == L_tri_par_nom

teste_tri_par_insertion_en_place()

À l'aide du code suivant, quelle type de relation de comparaison (stricte ou large) faut-il à votre donner pour que le tri implémenté par la fonction tri_par_insertion_en_place soit stable?

print("Pour tri_par_insertion_en_place:")
L = [(2,"A"), (2,"B"), (1,"C"), (2, "D"), (3,"E")]
print("  Avant tri:", L)
tri_par_insertion_en_place(L, comp_large_par_age)
print("  Après tri:", L)

Pour tri_par_insertion_en_place:
  Avant tri: [(2, 'A'), (2, 'B'), (1, 'C'), (2, 'D'), (3, 'E')]
  Après tri: [(1, 'C'), (2, 'A'), (2, 'B'), (2, 'D'), (3, 'E')]

print("Pour tri_par_insertion_en_place:")
L = [(2,"A"), (2,"B"), (1,"C"), (2, "D"), (3,"E")]
print("  Avant tri:", L)
tri_par_insertion_en_place(L, comp_stricte_par_age)
print("  Après tri:", L)

Pour tri_par_insertion_en_place:
  Avant tri: [(2, 'A'), (2, 'B'), (1, 'C'), (2, 'D'), (3, 'E')]
  Après tri: [(1, 'C'), (2, 'D'), (2, 'B'), (2, 'A'), (3, 'E')]

4. Tri partition-fusion (merge sort)

#+BEGIN_activite

Commencer par écrire une fonction fusion

acceptant trois arguments qui sont deux listes triées et une fonction de comparaison (celle pour lesquelles ces deux listes sont triées);
et qui retourne la fusion ces deux listes triée.

On testera consciencieusement cette fonction!

def fusion(L1, L2, fonction_de_comparaison):
    ???

def less_than_or_equal(x, y):
    return x <= y

def teste_fusion():
   L1 = [2]
   L2 = [1]
   res = sorted(L1+L2)
   assert res == fusion(L1, L2, less_than_or_equal)
   L1 = [1, 2, 4, 5]
   L2 = [0, 2, 3, 5, 6]
   res = sorted(L1+L2)
   assert res == fusion(L1, L2, less_than_or_equal)
   L1 = [1, 2, 4, 5, 6]
   L2 = [0, 2, 3, 5]
   res = sorted(L1+L2)
   assert res == fusion(L1, L2, less_than_or_equal)

teste_fusion()

def fusion(L1, L2, fonction_de_comparaison):
    i1, i2 = 0, 0
    L_res = []
    while i1 < len(L1) and i2 < len(L2):
        if fonction_de_comparaison(L1[i1], L2[i2]):
            L_res.append(L1[i1])
            i1 += 1
        else:
            L_res.append(L2[i2])
            i2 += 1
    return L_res + L1[i1:] + L2[i2:]

def less_than_or_equal(x, y):
    return x <= y

def teste_fusion():
   L1 = [2]
   L2 = [1]
   res = sorted(L1+L2)
   assert res == fusion(L1, L2, less_than_or_equal)
   L1 = [1, 2, 4, 5]
   L2 = [0, 2, 3, 5, 6]
   res = sorted(L1+L2)
   assert res == fusion(L1, L2, less_than_or_equal)
   L1 = [1, 2, 4, 5, 6]
   L2 = [0, 2, 3, 5]
   res = sorted(L1+L2)
   assert res == fusion(L1, L2, less_than_or_equal)

teste_fusion()

Écrire une fonction tri_partition_fusion_moults_copies

qui accepte deux arguments à savoir un tableau de une fonction de comparaison;
et qui retrourne uen copie de la liste triée.

On n'essaiera pas de minimiser le nombre de copies de listes effectuées!

def tri_partition_fusion_moults_copies(tab, fonction_de_comparaison):
    n = len(tab)
    if n <= 1:
        return tab
    ind_pivot = n // 2 
    tab_gauche_triee = tri_partition_fusion_moults_copies(tab[:ind_pivot],
                                            fonction_de_comparaison)
    tab_droite_triee = tri_partition_fusion_moults_copies(tab[ind_pivot:],
                                            fonction_de_comparaison)
    return fusion(tab_gauche_triee,
                  tab_droite_triee,
                  fonction_de_comparaison)

def teste_tri_partition_fusion_moults_copies():
   L = [(4, "a"), (2, "c"), (5, "b"), (0, "e")]
   res = [(0, "e"), (2, "c"), (4, "a"), (5, "b")]
   L_triee = tri_partition_fusion_moults_copies(L, comp_large_par_age)
   assert L_triee == res
   res = [(4, "a"), (5, "b"), (2, "c"), (0, "e")]
   L_triee = tri_partition_fusion_moults_copies(L, comp_large_par_nom)
   assert L_triee == res

teste_tri_partition_fusion_moults_copies()

5. Tri rapide ou tri pivot (quicksort sort)

Compléter la fonction pivot_bien_place(L, pivot, compare) qui vérifie si tous les éléments inférieures (pour la fonction de comparaison compare) à pivot sont placés en début de la liste L suivis des autres.

def pivot_bien_place(L, pivot, compare):
    i = 0
    while i < ?? and compare(??, ??):
        i+=1
    while i < ?? and ??==??:
        i+=1
    while i < ?? and not compare(??, ??):
        i+=1
    return ??

def less_than_or_equal(x, y):
    return x <= y

def teste_pivot_bien_place():
    L = [0, 3, 2, 4, 4, 5, 18, 19, 17, 21, 17]
    assert pivot_bien_place(L, 4, less_than_or_equal)
    assert pivot_bien_place(L, 5, less_than_or_equal)
    assert pivot_bien_place(L, 21, less_than_or_equal)
    assert pivot_bien_place(L, 0, less_than_or_equal)
    assert not pivot_bien_place(L, 2, less_than_or_equal)
    assert not pivot_bien_place(L, 18, less_than_or_equal)
    assert not pivot_bien_place(L, 17, less_than_or_equal)

teste_pivot_bien_place()

def pivot_bien_place(L, pivot, compare):
    i = 0
    while i < len(L) and compare(L[i], pivot):
        i+=1
    while i < len(L) and L[i]==pivot:
        i+=1
    while i < len(L) and not compare(L[i], pivot):
        i+=1
    return i == len(L)

def less_than_or_equal(x, y):
    return x <= y

def teste_pivot_bien_place():
    L = [0, 3, 2, 4, 4, 5, 18, 19, 17, 21, 17]
    assert pivot_bien_place(L, 4, less_than_or_equal)
    assert pivot_bien_place(L, 5, less_than_or_equal)
    assert pivot_bien_place(L, 21, less_than_or_equal)
    assert pivot_bien_place(L, 0, less_than_or_equal)
    assert not pivot_bien_place(L, 2, less_than_or_equal)
    assert not pivot_bien_place(L, 18, less_than_or_equal)
    assert not pivot_bien_place(L, 17, less_than_or_equal)

teste_pivot_bien_place()

Écrire une fonction place_pivot_1er_elmt_en_place_et_ret_index

def place_pivot_1er_elmt_en_place_et_ret_index(tab, ind_g, ind_d, compare):
    pivot = tab[ind_g]
    i = ind_g+1
    j = ind_d - 1
    while i <= j:
        while i < ind_d and compare(tab[i], pivot):
            i += 1
        while j > 0 and not compare(tab[j], pivot):
            j -= 1
        if i < j:
            tab[i], tab[j] = tab[j], tab[i]
            i += 1
            j -= 1
    tab[ind_g], tab[j] = tab[j], tab[ind_g]
    return j

def teste_place_pivot_premier_elmt_en_place():
    L = [4, 5]
    ind_pivot = place_pivot_1er_elmt_en_place_et_ret_index(L,
                                                           0, len(L),
                                                           less_than_or_equal)
    assert L == [4, 5]
    L = [5, 4]
    ind_pivot = place_pivot_1er_elmt_en_place_et_ret_index(L,
                                                           0, len(L),
                                                           less_than_or_equal)
    assert L == [4, 5]
    L = [4, 5, 3]
    ind_pivot = place_pivot_1er_elmt_en_place_et_ret_index(L,
                                                           0, len(L),
                                                           less_than_or_equal)
    assert L == [3, 4, 5]
    L = [4, 5, 2, 1, 6, 0, 7]
    L_init = L.copy()
    pivot = L[0]
    ind_g, ind_d = 0, 4
    ind_pivot = place_pivot_1er_elmt_en_place_et_ret_index(L,
                                                           ind_g, ind_d,
                                                           less_than_or_equal)
    assert L[ind_pivot] == pivot
    assert sorted(L_init[ind_g:ind_d]) == sorted(L[ind_g:ind_d]) # no fake dups, nothing lost nor created
    assert pivot_bien_place(L[ind_g:ind_d], pivot, less_than_or_equal)

teste_place_pivot_premier_elmt_en_place()

Écrire une fonction tri_rapide_en_place(tab, compare) qui trie le tableau passé en premier argument suivant le relation de comparaison passée en second argument en utilisant le tri rapide. On utilisera une fonction auxiliaire tri_rapide_en_place_aux comme dans le squelette ci-dessous.

def tri_rapide_en_place_aux(tab, ind_g, ind_d, compare):
    ??
    ind_piv = place_pivot_1er_elmt_en_place_et_ret_index(??,
                                                         ??, ??,
                                                         ??)
    tri_rapide_en_place_aux(??, ??, ??, ??)
    tri_rapide_en_place_aux(??, ??, ??, ??)

def tri_rapide_en_place(tab, compare):
    tri_rapide_en_place_aux(??, ??, ??, ??)

def teste_tri_rapide_en_place():
    L = [4, 5, 2, 1, 6, 0, 7]
    L_init = L.copy()
    tri_rapide_en_place(L, less_than_or_equal)
    assert L == sorted(L_init)

teste_tri_rapide_en_place()

def tri_rapide_en_place_aux(tab, ind_g, ind_d, compare):
    if ind_d <= ind_g + 1:
        return
    ind_piv = place_pivot_1er_elmt_en_place_et_ret_index(tab,
                                                         ind_g, ind_d,
                                                         compare)
    tri_rapide_en_place_aux(tab, ind_g, ind_piv, compare)
    tri_rapide_en_place_aux(tab, ind_piv+1, ind_d, compare)

def tri_rapide_en_place(tab, compare):
    tri_rapide_en_place_aux(tab, 0, len(tab), compare)

def teste_place_pivot_premier_elmt_en_place():
    L = [4, 5, 2, 1, 6, 0, 7]
    L_init = L.copy()
    tri_rapide_en_place(L, less_than_or_equal)
    assert L == sorted(L_init)

teste_place_pivot_premier_elmt_en_place()

6. Tri par comptage (bucket sort)

Compléter la fonction tri_par_comptage(L, compare).

def tri_par_comptage(L, compare):
    M = max(L)
    occur_list = [0]*M
    for elmt in L:
        occur_list[elmt] += 1
    res = [None]*len(L)
    i = 0
    for elmt in range(M):
        for nbr_occur in occur_list:
            res[i] = elmt
            i += 1
    return res


def teste_tri_par_comptage():
    L = [4, 3, 7, 2, 8, 5]
    assert tri_par_comptage(L, less_than_or_equal) == sorted(L)

teste_tri_par_comptage()

7. Complexité

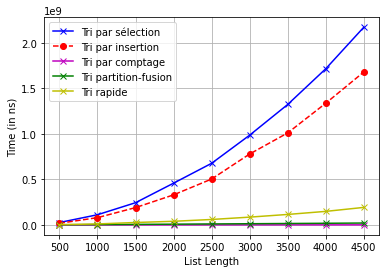
Executer le script ci-dessous après y avoir copié vos fonctions de tri (toutes testées) tri_par_selection_en_place_v1, tri_par_insertion_en_place, tri_par_comptage, tri_partition_fusion_moults_copies et tri_rapide_en_place. Cela est-il en accord avec le cours?

import time, gc
import numpy as np
import matplotlib.pyplot as plt

sorts = [
    {
        "name": "Tri par sélection",
        "sort_fun": lambda arr: tri_par_selection_en_place_v1(arr,less_than_or_equal),
        "style": "b-x",
    },
    {
        "name": "Tri par insertion",
        "sort_fun": lambda arr: tri_par_insertion_en_place(arr,less_than_or_equal),
        "style": "r--o",
    },
    {
        "name": "Tri par comptage",
        "sort_fun": lambda arr: tri_par_comptage(
            arr, less_than_or_equal),
        "style": "m-x",
    },
    {
        "name": "Tri partition-fusion",
        "sort_fun": lambda arr: tri_partition_fusion_moults_copies(
            arr, less_than_or_equal),
        "style": "g-x",
    },
    {
        "name": "Tri rapide",
        "sort_fun": lambda arr: tri_rapide_en_place(
            arr, less_than_or_equal),
        "style": "y-x",
    }
]

N = 500
elements = np.array([i*N for i in range(1, 10)])

plt.xlabel('List Length')
plt.ylabel('Time (in ns)')

a, b = 1, 10
for sort in sorts:
    data = [(i,list(np.random.randint(10, size = i * N)))
            for i in range(a, b)]
    gc.disable()
    times = list()
    start_all = time.perf_counter_ns()
    for i, L in data:
        start = time.perf_counter_ns()
        sort["sort_fun"](L)
        end = time.perf_counter_ns()
        times.append(end - start)
    end_all = time.perf_counter_ns()
    gc.enable()
    gc.collect()
    plt.plot(elements, times, sort["style"], label = sort["name"])

plt.grid()
plt.legend()
plt.show()