‎

Créer un sous-dossier «TP11» dans le dossier «TP_informatique_commune» de votre repertoire personnel
Si on vous demande d'écrire un script python à la question 3\c) de l'activité 2 du TP 7 vous enregistrez ce script dans un fichier nommé «tp07_act02_q03c.py». Remarquez que l'on utilisera toujours deux chiffres décimaux pour représenter les entiers et que l'on va toujours du général vers le particulier car ainsi l'ordre alphabétique correspond à l'ordre tri chronologique.
- On rendra son code modulaire en utilisant systématiquement des fonctions
- On testera toutes ses fonctions

1. Préléminaires

Compléter la définition suivante pour que la fonction mat_adj_vers_dict_succ pour qu'elle retourne un dictionnaire des successeurs représentant le graphe de matrice d'adjacence donnée en arguments

import numpy as np

def mat_adj_vers_dict_succ(A):
   n, p = A.shape
   assert n == ??
   d = ??
   for i in range(n):
      d[i] = ??
      for j in range(n):
         if A[i,j] == ??:
            d[??].append(??)
   return ??

def teste_mat_adj_vers_dict_succ():
   A = np.array([[0,1,0], [1,0,0], [0,1,0]])
   d = mat_adj_vers_dict_succ(A)
   assert d[0] == ??
   assert d[1] == ??
   assert d[2] == ??
   A = np.array([[1,1,0], [1,0,1], [0,1,1]])
   d = mat_adj_vers_dict_succ(A)
   assert sorted(d[0])==??
   assert sorted(d[1])==??
   assert sorted(d[2])==??

teste_mat_adj_vers_dict_succ()

Écrire une fonction mat_adj_vers_dict_pred pour qu'elle retourne un dictionnaire des prédecesseurs représentant le graphe de matrice d'adjacence donnée en argument.

1. Écrire une fonction compare_par_age qui accepte deux éléments que l'on supposera être des couples (de type tuple ou list) formés d'une valeur numérique (appelé âge) et d'une valeur de type chaîne de caractères (appelé nom) et qui retourne True si le premier est d'âge inférieur ou égal au second et False sinon.
2. Écrire une fonction similaire compare_par_nom qui compare cette fois par ordre lexicographique des noms.
3. Écrire une fonction liste_est_triee qui accepte deux arguments qui sont
  - une liste L d'éléments de types homogènes;
  - une fonction de compariason compare qui accepte deux élements supposés du type des éléments formant la liste L et qui retourne True ou False suivant que le premier est considérée inférieur ou égal au second ou non.
  et qui retourne True si la liste L est triée et False sinon. Ainsi par exemple avec
  
  L=[(1,"B"), (2,"A"), (3,"C")]
  - l'appel liste_est_triee(L, compare_par_age) doit renvoyer True;
  - alors que liste_est_triee(L, compare_par_nom) doit renvoyer False;
  On testera (évidemment) cette fonction!

2. Labyrinthes et graphes

Ici un labyrinthe est représenté par un tableau de dimension deux de taille \(n\times{}p\) où les cellules à 0 représentent les cellules libres et les autres sont à 1 et représentent des murs. À un tel labyrinthe on associe un graphe orienté (mais symétrique) dont les sommets sont les tuples (i,j) avec 0<=i<n et 0<=j<p qui sont libres et où les sommets adjacents au sommet \((i,j)\) sont les sommets libres de la forme \((i\pm1,j)\) et \((i,j\pm1)\) (en particulier il n'y a pas de mouvement en diagonal: les sommets \((i,j)\) et \((i\pm1,j\pm1)\) ne sont jamais adjacents).

Vérifier que le programme ci-dessous affiche bien l'image qui lui suit

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def plot_maze_and_paths(maze, path_list, ax = None):
    ax = plt.gca() if ax is None else ax
    colors = [[0,1,0], [0,0,0], [0,0,1]]
    maze = maze.copy() # prevents side-effects
    for path in path_list:
        for s in path:
            i, j = s
            assert maze[i, j] == 0
            maze[i, j] = 2
    ax.set_xticks([], minor=False)
    ax.set_yticks([], minor=False)
    ax.set_aspect('equal') #set the x and y axes to the same scale
    ax.invert_yaxis() #invert the y-axis so the first row of data is at the top
    ax.pcolormesh(maze, vmin=0, vmax=2, cmap=ListedColormap(colors))

maze = np.array([
    [0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0],
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
])
path_1 = [(1,5), (1,6), (0,6), (0,7), (0,8), (1,8)]
plot_maze_and_paths(maze, [path_1])
plt.show()

Compléter la fonction maze_to_succdict ci-dessous afin qu'elle retourne le graphe du labyrinthe passé en argument où

le labyrinthe est représenté par un tableau de dimension deux dont les cases libres sont représentées par des 0 et les cases occupées (murs) par des 1;

le graphe retourné est représenté par un dictionnaire de dictionnaires d'associations successeurs/distance.

def maze_to_succdict(maze):
    n, p = maze.shape
    succ_dict = {}
    for i in range(n):
        for j in range(p):
            s = (i,j)
            if maze[i, j] != 0:
                ??
            succ_s_dict = {}
            for di, dj in [(1,0), (0,1), (-1,0), ??]:
                i_adj, j_adj = i+di, j+dj
                i_adj_asmissible = i_adj >= 0 and i_adj < n 
                j_adj_asmissible = j_adj >= 0 and j_adj < p
                if not i_adj_asmissible ?? not j_adj_asmissible ?? maze[i_adj, j_adj] != 0:
                    ??
                succ_s_dict[(i_adj, j_adj)] = 1
            succ_dict[s] = ??
    return ??

def teste_maze_to_succdict():
    maze = np.array([
        [0, 0, 0],
        [1, 1, 1],
        [0, 0, 1],
    ])
    res = {
        (0, 0): {(0, 1): 1},
        (0, 1): {??},
        (0, 2): {??},
        (2, 0): {(2, 1): 1},
        (2, 1): {(2, 0): 1},
    }
    assert maze_to_succdict(maze) == res

teste_maze_to_succdict()

3. Un algorithme naïf

Un premier algorithme naif (juste mais peu efficace) pour calculer les distances minimales en partant d'un sommet start fixé est

de partir d'une liste dist_list de distances toutes infines sauf celle correspondant au sommet start qui vaut 0;
puis dans une boucle on teste "tous les potentiels raccourcis" et si on trouve un vrai raccourci alors on modifie dist_list en conséquence. Plus précisément la boucle
- est effectuée tant que la liste dist_list est modifiée;
- et si on trouve deux sommets i_tmp et i2 tels que dist_list[i_tmp]+A[i_tmp][i2]<dist_list[i2] (on a trouvé un raccourci en passant par i_tmp) alors on modifie dist_list[j] en conséquence.

Enfin, comme on veut pouvoir récupérer un chemin de longueur minimal partant de start et arrivant à un autre sommet quelconque on maintient un dictinnaire d'association sommet_somemt appelé parent_dict tel que pour tout sommet s l'expressions parent_dict[s] renvoie le sommet précédent s sur un plus court chemin allant de start à s.

Compléter la fonction suivante pour qu'elle implémente cet algorithme où le graphe est donné sous la forme d'un dictionnaire de dictionnaires d'associations successeur/longueur.

def algo_naif_dist_a_sommet_fixe_succdict(G_succ, i):
    n = len(G_succ)
    assert i in G_succ
    dist_dict = {s: ?? for s in G_succ}
    parent_dict = {s: ?? for s in G_succ}
    dist_dict[i] = ??
    something_changed = ??
    while something_changed:
        something_changed = ??
        for s_tmp in G_succ:
            for s2 in G_succ[s_tmp]:
                other_dist = dist_dict[s_tmp]+G_succ[??][s2]
                if other_dist ?? dist_dict[s2]:
                    dist_dict[s2] = ??
                    parent_dict[s2] = ??
                    something_changed = ??
    return parent_dict, dist_dict

def teste_algo_naif_dist_a_sommet_fixe_succdict():
    G = {
        "A": {"B": 9, "C": 1},
        "B": {"A": 1, "C": 1},
        "C": {"A": 1, "B": 1}
    }
    par_d, dist_d = algo_naif_dist_a_sommet_fixe_succdict(G, "A")
    assert dist_d == {"A": ??, "B": ??, "C": ??}
    assert par_d == {"A": ??, "B": ??, "C": ??}
    G["A"]["B"] = 1
    par_d, dist_d = algo_naif_dist_a_sommet_fixe_succdict(G, "A")
    assert dist_d == {"A": ??, "B": ??, "C": ??}
    assert par_d == {"A": ??, "B": ??, "C": ??}

teste_algo_naif_dist_a_sommet_fixe_succdict()

(seulement si vous êtes en avance) Compléter la fonction algo_naif_dist_a_sommet_fixe_matadj ci-dessous pour qu'elle implémente le même algorithme que algo_naif_dist_a_sommet_fixe_succdict mais où le graphe est donné sous la forme d'une matrice d'adjacence.

def algo_naif_dist_a_sommet_fixe_matadj(A, i):
    n, p = A.shape
    assert n==p
    assert 0 <= i and i < n
    dist_list = [??] * n
    dist_list[i] = ??
    something_changed = ??
    while something_changed:
        something_changed = ??
        for i2 in range(??):
            for i_tmp in range(??):
                other_dist = dist_list[i_tmp]+A[i_tmp][i2]
                if ?? < ??:
                    dist_list[i2] = other_dist
                    something_changed = True
    return ??

def teste_algo_naif_dist_a_sommet_fixe_matadj():
    A = np.array([[0, 9, 1], [1, 0, 1], [1, 1, 0]])
    d = algo_naif_dist_a_sommet_fixe_matadj(A, 0)
    assert d == ??
    A = np.array([[0, 2, np.inf, np.inf],
                  [3, 0, np.inf, np.inf],
                  [np.inf, np.inf, 0, 4],
                  [np.inf, np.inf, 5, 0]])
    d = algo_naif_dist_a_sommet_fixe_matadj(A, 0)
    assert d == ??
    A[0,2] = 121
    d = algo_naif_dist_a_sommet_fixe_matadj(A, 0)
    assert d == ??

teste_algo_naif_dist_a_sommet_fixe_matadj()

Compléter la fonction create_path_using_parent_dict ci-dessous pour qu'étant donné un tableau de prédécesseurs (la valeur particulière None signifiant que le somemt n'a pas de prédécesseur) et un sommet elle retourne le chemin terminant en ce sommet dont la relation sommet à prédesseur est déterminée par le tableau. On s'arrêtera au premier sommet sans prédecesseur.

Vérifier alors que le programme suivant affiche tour à tour les image ci-dessous

maze = np.array([
    [0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0],
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
])
G_succ = maze_to_succdict(maze)
start = (0, 0)
par_d, dist_d = algo_naif_dist_a_sommet_fixe_succdict(G_succ, start)
# ---
goal = (3, 10)
path = create_path_using_parent_dict(par_d, goal)
plot_maze_and_paths(maze, [path])
plt.show()
# ---
goal = (5, 10)
path = create_path_using_parent_dict(par_d, goal)
plot_maze_and_paths(maze, [path])
plt.show()

4. Files d'attentes

#+BEGIN_activite

Compléter la fonction de test suivante pour tous les tests (du module heapq) passent.

import heapq

def teste_module_heapq():
    pq = []
    for prio, elmt in [(6,"a"), (4,"b"), (5,"c"), (7,"d")]:
        heapq.heappush(pq, (prio, elmt))
    prio, elmt = heapq.heappop(pq)
    assert prio == ?? and elmt == ??
    prio, elmt = heapq.heappop(pq)
    assert prio == ?? and elmt == ??
    heapq.heappush(pq, (8, "e"))
    heapq.heappush(pq, (0, "f"))
    heapq.heappush(pq, (9, "g"))
    prio, elmt = heapq.heappop(pq)
    assert prio == ?? and elmt == ??

teste_module_heapq()

5. Algorithme de Dijkstra

Compléter la fonction suivante pour qu'elle implémente l'algorithme de Dijkstra. On utilisera la structure de file de priorité implémentée par-dessus le type list par le module heapq. Ainsi

la liste pq sera vu comme une file de priorité;
pour cela on naccedera pas directment à ses éléments (cela casserai sans doute la file de priorité!) mais
- on utilisera heapq.heappush(pq, (priority, node)) pour ajouter une élément node de priorité priority à la file de priorité pq;
- on utilisera heapq.heappop(pq) pour récupérer l'élément de priorité minimale (..) de la file de priorité pq.

import heapq

def dijkstra_succdict(G_succdict, start, goal):
    n = len(G_succdict)
    assert start in G_succdict
    node_dist_dict = {s: ?? for s in G_succdict}
    node_dist_dict[start] = ??
    was_visited_list = {s: ?? for s in G_succdict}
    was_visited_list[start] = ??
    node_to_parent = {s: ?? for s in G_succdict}
    pq = []
    priority, node = 0, start
    heapq.heappush(pq, (priority, node))
    while len(pq) > 0:
        _, node = heapq.heappop(pq)
        was_visited_list[node] = ??
        if node == goal:
            return node_to_parent, node_dist_dict[goal]
        for adj_node in G_succdict[node]:
            if was_visited_list[adj_node]:
                ??
            new_dist = node_dist_dict[node] + G_succdict[??][??]
            if new_dist ?? node_dist_dict[adj_node] :
                node_to_parent[adj_node] = ??
                node_dist_dict[adj_node] = ??_dist
                heapq.heappush(pq, (new_dist, adj_node))
    return None # no path from start to goal 

def teste_dijkstra_succdict():
    G_succdict = {
        "A": {"B": 1,"C": 3,"D": 4},
        "B": {"A": 1,"C": 1,"D": 4},
        "C": {"A": 1,"B": 1,"D": 1},
        "D": {"A": 1,"B": 1,"C": 1},
    }
    par_dict, dist = dijkstra_succdict(G_succdict, "A", "D")
    assert dist == ??
    assert par_dict == {"A": ??, "B": ??, "C": ??, "D": ??}
    G_succdict = {
        "A": {"A": 0,"B": 2},
        "B": {"A": 3,"B": 0},
        "C": {"C": 0, "D": 4},
        "D": {"C": 5, "D": 0},
    }
    res = dijkstra_succdict(G_succdict, "A", "C")
    assert res == ??

teste_dijkstra_succdict()

azaz

maze = np.array([
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
    [0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
])
G_succ = maze_to_succdict(maze)
start = (4, 5)
# ---
goal = (5, 12)
par_dict, dist = dijkstra_succdict(G_succ, start, goal)
path = create_path_using_parent_dict(par_dict, goal)
plot_maze_and_paths(maze, [path])
plt.show()
# ---
goal = (10, 12)
par_dict, dist = dijkstra_succdict(G_succ, start, goal)
path = create_path_using_parent_dict(par_dict, goal)
plot_maze_and_paths(maze, [path])
plt.show()

6. Algorithme A* (A star)

Pour calculer la longueur du plus court chemin d'un sommet "A" à un sommet "B" l'algorithme de Djikstra calcule les distances à et en partant de "A" de tous les sommets.
Ceci est très lourd en temps et en mémoire.
Supposons que l'on sache que d("A","B") <= 10. Si à un moment ou à un autre on déterminé que d("A","D") > 10 alors il n'est pas nécessaire de considéré les chemin qui vont de "A" à "b" en passant par "D"!
Pour cela on suppose donnée uen heuristique h (facile à calculer) telle que h<=d Ainsi si h("A","B")<=10 alors d("A","B")<=10. Si à un moment ou à un autre on déterminé que d("A","D") > 10 alors il n'est pas nécessaire de considéré les chemin qui vont de "A" à "b" en passant par "D"!

import math

def null_heuristic(P, Q):
    return 0

def manhattan_heuristic(P, Q):
    return abs(P[0]-Q[0])+abs(P[1]-Q[1])

def as_the_crow_flies_heuristic(P, Q):
    return ((P[0]-Q[0])**2+(P[1]-Q[1])**2)**(1/2)


def favor_good_diags_heuristic(P, Q):
    return max(abs(P[0]-Q[0]),abs(P[1]-Q[1]))

def favor_good_horiz_heuristic(P, Q):
    return abs(P[1]-Q[1])

def favor_good_vert_heuristic(P, Q):
    return abs(P[0]-Q[0])

maze = np.array([
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
])
start, goal = (10, 10), (10, 24)
data = [
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": null_heuristic,
     },
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": manhattan_heuristic,
     },
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": as_the_crow_flies_heuristic,
     },
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": favor_good_diags_heuristic,
     },
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": favor_good_horiz_heuristic,
     },
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": favor_good_vert_heuristic,
     },
    ]

data_len = len(data)
n, p = 2, 3
fig, axs = plt.subplots(nrows=n, ncols=p, figsize=(15,15))

for i, d in enumerate(data):
    maze = d["maze"]
    heuristic = d["heuristic"]
    G_succ = maze_to_succdict(maze)
    par_dict, dist = astar_succdict(G_succ, start, goal, heuristic)
    path = create_path_using_parent_dict(par_dict, goal)
    n, p = i//3, i%3
    ax = axs[i//3, i%3]
    plot_maze_and_paths(maze, [path], ax)
    ax.set_title(heuristic.__name__)

plt.tight_layout()
plt.show()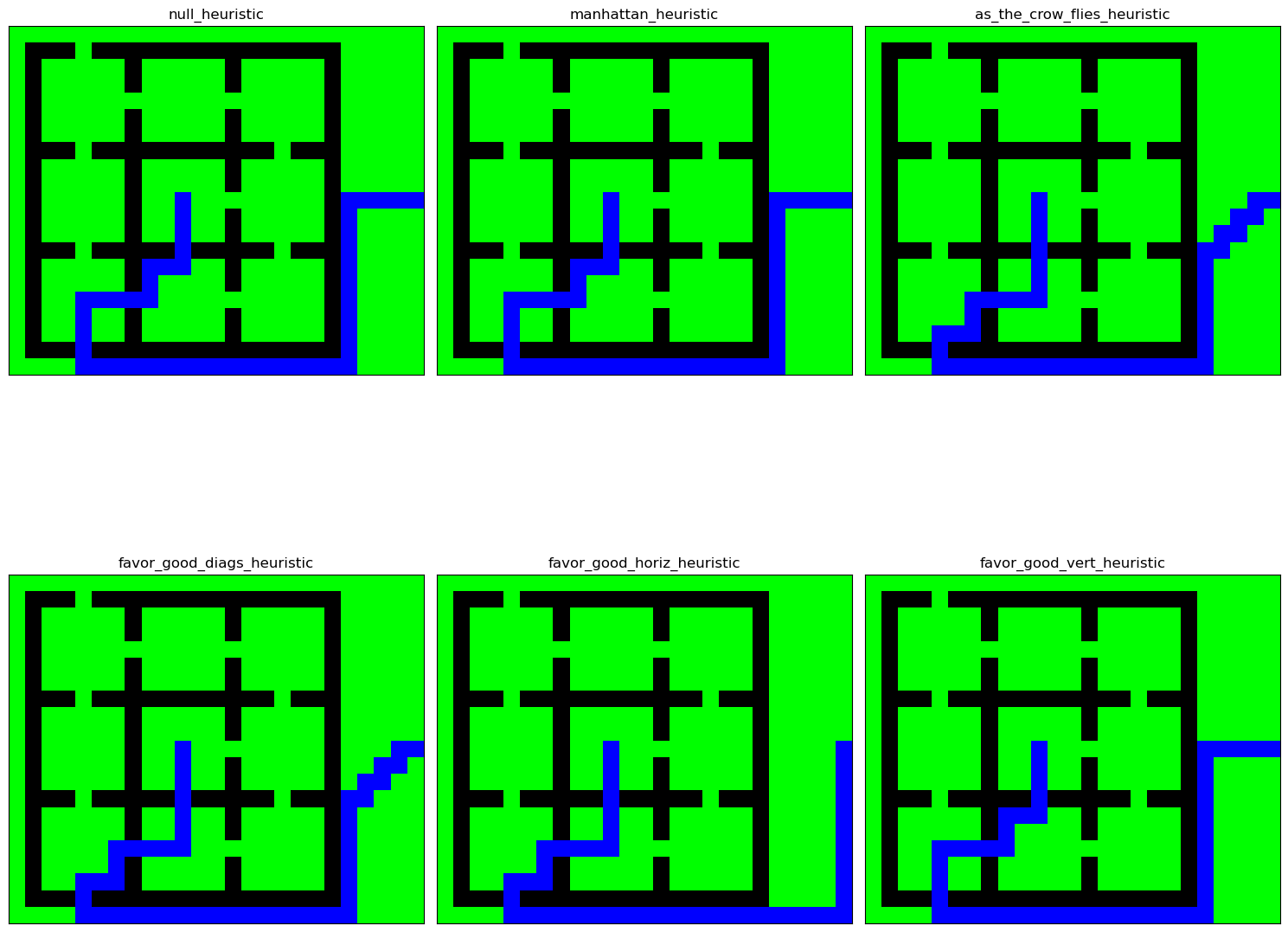

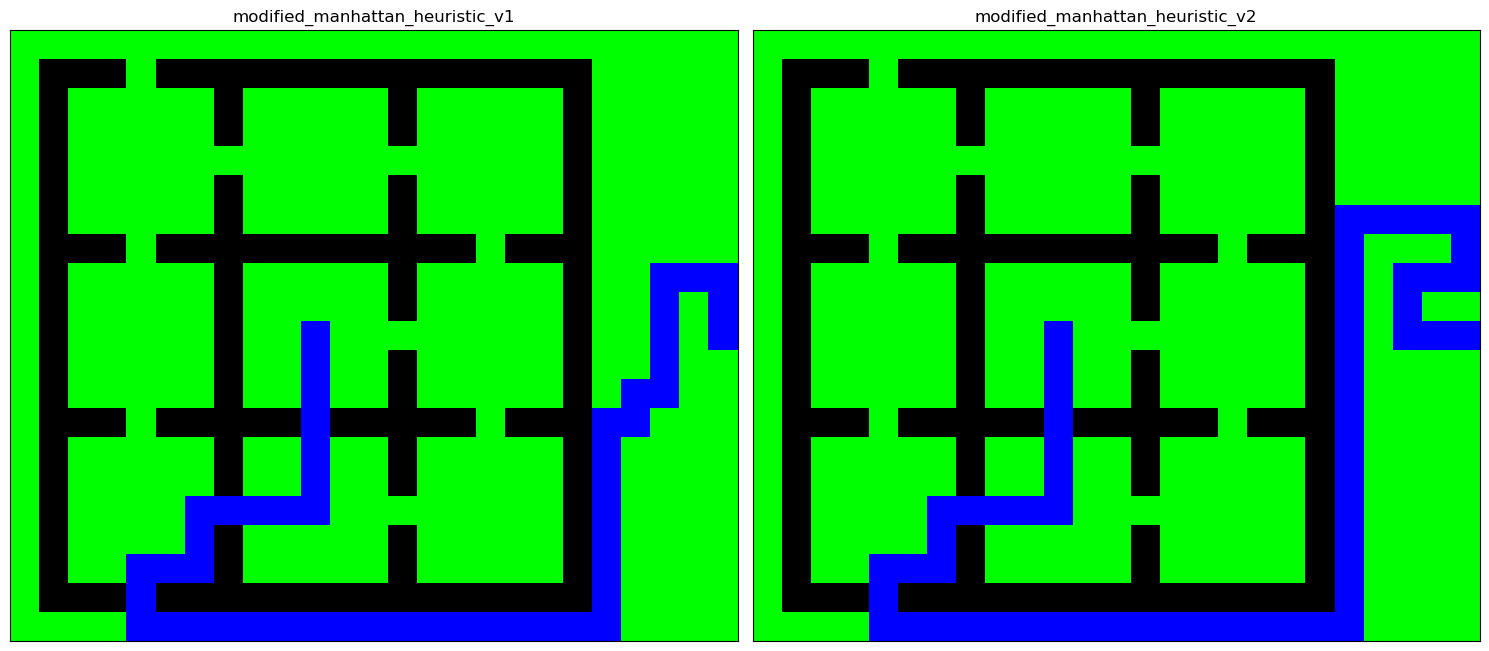
On propose deux (mauvaises) heuristiques obtenues en modifiant une bonne heuristique à l'arrivée. vérifier que vous obtenez les graphiques ci-dessous;

import math

def modified_manhattan_heuristic_v1(P, Q):
    addtve_mask_near_goal = [
        [-40,-40,-40, 99, 99],
        [-40, 99,-40, 99, 99],
        [-40, 99,-40, 99, 99],
        [-40, 99, 99, 99, 99],
        [-40, 99, 99, 99, 99],
        ]
    n = len(addtve_mask_near_goal) #5
    rad = n // 2 #2
    if abs(P[0]-Q[0]) > rad or abs(P[1]-Q[1]) > rad:
        return max(abs(P[0]-Q[0]),abs(P[1]-Q[1]))
    di, dj = P[0]-Q[0], P[1]-Q[1]
    add = addtve_mask_near_goal[di+rad][dj+rad]
    return add+max(abs(P[0]-Q[0]),abs(P[1]-Q[1]))

def modified_manhattan_heuristic_v2(P, Q):
    addtve_mask_near_goal = [
        [-10, -10, -10, -10, -10, 99, 99, 99, 99],
        [-10,  99,  99,  99, -10, 99, 99, 99, 99],
        [-10,  99, -10, -10, -10, 99, 99, 99, 99],
        [-10,  99, -10,  99,  99, 99, 99, 99, 99],
        [-10,  99, -10, -10, -10, 99, 99, 99, 99],
        [-10,  99,  99,  99,  99, 99, 99, 99, 99],
        [-10,  99,  99,  99,  99, 99, 99, 99, 99],
        [-10,  99,  99,  99,  99, 99, 99, 99, 99],
        [-10,  99,  99,  99,  99, 99, 99, 99, 99],
        ]
    n = len(addtve_mask_near_goal) #9
    rad = n // 2 #4
    if abs(P[0]-Q[0]) > rad or abs(P[1]-Q[1]) > rad:
        return max(abs(P[0]-Q[0]),abs(P[1]-Q[1]))
    di, dj = P[0]-Q[0], P[1]-Q[1]
    add = addtve_mask_near_goal[di+rad][dj+rad]
    return add+max(abs(P[0]-Q[0]),abs(P[1]-Q[1]))


maze = np.array([
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
])
start, goal = (10, 10), (10, 24)
data = [
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": modified_manhattan_heuristic_v1,
     },
    {
        "maze": maze,
        "start": start,
        "goal": goal,
        "heuristic": modified_manhattan_heuristic_v2,
     },
    ]

data_len = len(data)
n, p = 1, 2
fig, axs = plt.subplots(nrows=n, ncols=p, figsize=(15,15))

for i, d in enumerate(data):
    maze = d["maze"]
    heuristic = d["heuristic"]
    G_succ = maze_to_succdict(maze)
    par_dict, dist = astar_succdict(G_succ, start, goal, heuristic)
    path = create_path_using_parent_dict(par_dict, goal)
    ax = axs[i]
    plot_maze_and_paths(maze, [path], ax)
    ax.set_title(heuristic.__name__)

plt.tight_layout()
plt.show()