‎

Créer un sous-dossier «TP11» dans le dossier «TP_informatique_commune» de votre repertoire personnel
Si on vous demande d'écrire un script python à la question 3\c) de l'activité 2 du TP 7 vous enregistrez ce script dans un fichier nommé «tp07_act02_q03c.py». Remarquez que l'on utilisera toujours deux chiffres décimaux pour représenter les entiers et que l'on va toujours du général vers le particulier car ainsi l'ordre alphabétique correspond à l'ordre tri chronologique.
- On rendra son code modulaire en utilisant systématiquement des fonctions
- On testera toutes ses fonctions

1. Préléminaires

#+BEGIN_activite

Compléter la définition suivante pour que la fonction mat_adj_vers_dict_succ pour qu'elle retourne un dictionnaire des successeurs représentant le graphe de matrice d'adjacence donnée en arguments

import numpy as np

def mat_adj_vers_dict_succ(A):
   n, p = A.shape
   assert n == ??
   d = ??
   for i in range(n):
      d[i] = ??
      for j in range(n):
         if A[i,j] == ??:
            d[??].append(??)
   return ??

def teste_mat_adj_vers_dict_succ():
   A = np.array([[0,1,0], [1,0,0], [0,1,0]])
   d = mat_adj_vers_dict_succ(A)
   assert d[0] == ??
   assert d[1] == ??
   assert d[2] == ??
   A = np.array([[1,1,0], [1,0,1], [0,1,1]])
   d = mat_adj_vers_dict_succ(A)
   assert sorted(d[0])==??
   assert sorted(d[1])==??
   assert sorted(d[2])==??

teste_mat_adj_vers_dict_succ()

Écrire une fonction mat_adj_vers_dict_pred pour qu'elle retourne un dictionnaire des prédecesseurs représentant le graphe de matrice d'adjacence donnée en argument.

Vérifier que le code ci-dessous affiche l'image qui lui suit

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from networkx.drawing.nx_pydot import graphviz_layout

def draw_weighted_digraph_dict_of_dict(graph, layout="spring_layout", root=None):
    graph_for_nx = {
        n: {
            succ: {"weight": weight} for succ, weight in d.items()
        } for n, d in graph.items()
    }
    G = nx.DiGraph(graph_for_nx)
    if layout == "spring_layout":
        pos = nx.spring_layout(G, seed=5) # seed for reproducible plots...
    else:
        pos = graphviz_layout(G, prog=layout, root=root)
    nx.draw(G, pos, with_labels=True, font_weight='bold')
    edge_labels = nx.get_edge_attributes(G,"weight")
    nx.draw_networkx_edge_labels(G, pos,
                                 edge_labels = edge_labels,
                                 font_weight='bold')

graph = {
    'A' : {'B': 5, 'C': 2},
    'B' : {'C': 1},
    'C' : {'A': 3, 'B': 8}
}
draw_weighted_digraph_dict_of_dict(graph)
plt.show()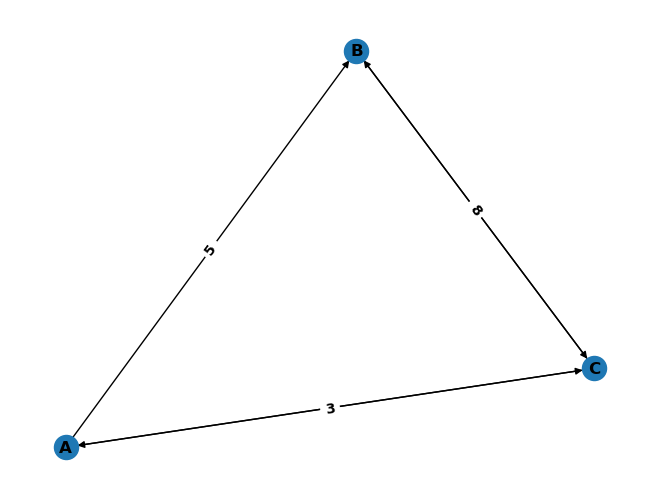

Vérifier que le code ci-dessous affiche l'image qui lui suit

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from networkx.drawing.nx_pydot import graphviz_layout

def draw_digraph_dict_of_list(graph, layout="spring_layout", root=None):
    G = nx.DiGraph(graph)
    if layout == "spring_layout":
        pos = nx.spring_layout(G, seed=5) # seed for reproducible plots...
    else:
        pos = graphviz_layout(G, prog=layout, root=root)
    nx.draw(G, pos, with_labels=True, font_weight='bold')
    nx.draw(G, pos, with_labels=True, font_weight='bold')

graph = {
    'A' : ['B', 'C'],
    'B' : ['C'],
    'C' : ['A', 'B'],
}
draw_digraph_dict_of_list(graph)
plt.show()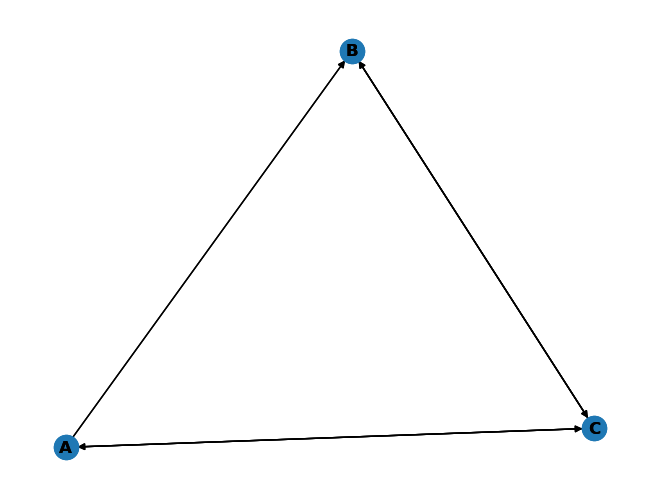

Compléter la fonction create_path_using_parent_dict ci-dessous pour qu'étant donné un tableau de prédécesseurs (la valeur particulière None signifiant que le somemt n'a pas de prédécesseur) et un sommet elle retourne le chemin terminant en ce sommet dont la relation sommet à prédesseur est déterminée par le tableau. On s'arrêtera au premier sommet sans prédecesseur.

def create_path_using_parent_dict(parent_dict, goal):
    path, s = ??, goal
    while ?? is not None:
        ??.append(??)
        s = parent_dict[s]
        assert ?? not in ?? # no loop
    return list(reversed(path))

def teste_create_path_using_parent_dict():
    # A -> C -> B -> E ; D
    parent_dict = {
        "A": None,
        "B": "C",
        "C": "A",
        "D": None,
        "E": "B"
    }
    goal = "E"
    path = create_path_using_parent_dict(parent_dict, goal)
    assert path == [??, ??, ??, "E"]

teste_create_path_using_parent_dict()

Dans cette section on ne s'intéresse qu'aux graphes non orienté #+BEGIN_activite

import numpy as np

def mat_adj_vers_dict_succ(A):
   n, p = A.shape
   assert n == ??
   d = ??
   for i in range(n):
      d[i] = ??
      for j in range(n):
         if A[i,j] == ??:
            d[??].append(??)
   return ??

def teste_mat_adj_vers_dict_succ():
   A = np.array([[0,1,0], [1,0,0], [0,1,0]])
   d = mat_adj_vers_dict_succ(A)
   assert d[0] == ??
   assert d[1] == ??
   assert d[2] == ??
   A = np.array([[1,1,0], [1,0,1], [0,1,1]])
   d = mat_adj_vers_dict_succ(A)
   assert sorted(d[0])==??
   assert sorted(d[1])==??
   assert sorted(d[2])==??

teste_mat_adj_vers_dict_succ()

Écrire une fonction mat_adj_vers_dict_pred pour qu'elle retourne un dictionnaire des prédecesseurs représentant le graphe de matrice d'adjacence donnée en argument.

Vérifier que le code ci-dessous affiche l'image qui lui suit

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from networkx.drawing.nx_pydot import graphviz_layout

def draw_weighted_digraph_dict_of_dict(graph, layout="spring_layout", root=None):
    graph_for_nx = {
        n: {
            succ: {"weight": weight} for succ, weight in d.items()
        } for n, d in graph.items()
    }
    G = nx.DiGraph(graph_for_nx)
    if layout == "spring_layout":
        pos = nx.spring_layout(G, seed=5) # seed for reproducible plots...
    else:
        pos = graphviz_layout(G, prog=layout, root=root)
    nx.draw(G, pos, with_labels=True, font_weight='bold')
    edge_labels = nx.get_edge_attributes(G,"weight")
    nx.draw_networkx_edge_labels(G, pos,
                                 edge_labels = edge_labels,
                                 font_weight='bold')

graph = {
    'A' : {'B': 5, 'C': 2},
    'B' : {'C': 1},
    'C' : {'A': 3, 'B': 8}
}
draw_weighted_digraph_dict_of_dict(graph)
plt.show()

Vérifier que le code ci-dessous affiche l'image qui lui suit

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from networkx.drawing.nx_pydot import graphviz_layout

def draw_digraph_dict_of_list(graph, layout="spring_layout", root=None):
    G = nx.DiGraph(graph)
    if layout == "spring_layout":
        pos = nx.spring_layout(G, seed=5) # seed for reproducible plots...
    else:
        pos = graphviz_layout(G, prog=layout, root=root)
    nx.draw(G, pos, with_labels=True, font_weight='bold')
    nx.draw(G, pos, with_labels=True, font_weight='bold')

graph = {
    'A' : ['B', 'C'],
    'B' : ['C'],
    'C' : ['A', 'B'],
}
draw_digraph_dict_of_list(graph)
plt.show()

def create_path_using_parent_dict(parent_dict, goal):
    path, s = ??, goal
    while ?? is not None:
        ??.append(??)
        s = parent_dict[s]
        assert ?? not in ?? # no loop
    return list(reversed(path))

def teste_create_path_using_parent_dict():
    # A -> C -> B -> E ; D
    parent_dict = {
        "A": None,
        "B": "C",
        "C": "A",
        "D": None,
        "E": "B"
    }
    goal = "E"
    path = create_path_using_parent_dict(parent_dict, goal)
    assert path == [??, ??, ??, "E"]

teste_create_path_using_parent_dict()

2. Labyrinthes et graphes

Ici un labyrinthe est représenté par un tableau de dimension deux de taille \(n\times{}p\) où les cellules à 0 représentent les cellules libres et les autres sont à 1 et représentent des murs. À un tel labyrinthe on associe un graphe orienté (mais symétrique) dont les sommets sont les tuples (i,j) avec 0<=i<n et 0<=j<p qui sont libres et où les sommets adjacents au sommet \((i,j)\) sont les sommets libres de la forme \((i\pm1,j)\) et \((i,j\pm1)\) (en particulier il n'y a pas de mouvement en diagonal: les sommets \((i,j)\) et \((i\pm1,j\pm1)\) ne sont jamais adjacents).

Vérifier que le programme ci-dessous affiche bien l'image qui lui suit

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def plot_maze_and_paths(maze, path_list, ax = None):
    ax = plt.gca() if ax is None else ax
    colors = [[0,1,0], [0,0,0], [0,0,1]]
    maze = maze.copy() # prevents side-effects
    ax.set_xticks([], minor=False)
    ax.set_yticks([], minor=False)
    ax.set_aspect('equal') #set the x and y axes to the same scale
    ax.invert_yaxis() #invert the y-axis so the first row of data is at the top
    ax.pcolormesh(maze, vmin=0, vmax=2, cmap=ListedColormap(colors))
    for path in path_list:
        for p in range(len(path)):
            s = path[p]
            i, j = s
            if p == len(path)-1:
                ax.text(j+1/2, i+1/2, "G", ha="center", va="center")
                continue
            if p == 0:
                ax.text(j+1/2, i+1/2, "S", ha="center", va="center")
            s_next = path[p+1]
            i_n, j_n = s_next
            di = (i_n-i)/2
            dj = (j_n-j)/2
            ax.arrow(j+1/2-dj/2, i+1/2-di/2, dj, di, width=0.1, color="red")
            # maze[i, j] = 2

maze = np.array([
    #0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12, 
    [0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0], #  0
    [0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0], #  1
    [0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0], #  2
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0], #  3
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0], #  4
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0], #  5
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0], #  6
    [0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0], #  7
    [0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0], #  8
    [0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0], #  9
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], # 10
])
path_1 = [(1,5), (1,6), (0,6), (0,7), (0,8), (1,8)]
plot_maze_and_paths(maze, [path_1])
plt.show()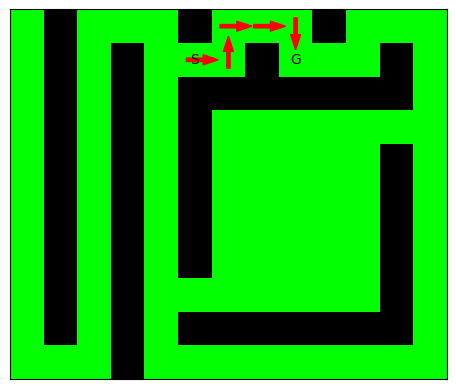

Compléter la fonction maze_to_succdict ci-dessous afin qu'elle retourne le graphe du labyrinthe passé en argument où

le labyrinthe est représenté par un tableau de dimension deux dont les cases libres sont représentées par des 0 et les cases occupées (murs) par des 1;

le graphe retourné est représenté par un dictionnaire de dictionnaires d'associations successeurs/distance.

def maze_to_succdict(maze):
    n, p = maze.shape
    succ_dict = {}
    for i in range(n):
        for j in range(p):
            s = (i,j)
            if maze[i, j] != 0:
                ??
            succ_s_dict = {}
            for di, dj in [(1,0), (0,1), (-1,0), ??]:
                i_adj, j_adj = i+di, j+dj
                i_adj_asmissible = i_adj >= 0 and i_adj < n 
                j_adj_asmissible = j_adj >= 0 and j_adj < p
                if not i_adj_asmissible ?? not j_adj_asmissible ?? maze[i_adj, j_adj] != 0:
                    ??
                succ_s_dict[(i_adj, j_adj)] = 1
            succ_dict[s] = ??
    return ??

def teste_maze_to_succdict():
    maze = np.array([
        [0, 0, 0],
        [1, 1, 1],
        [0, 0, 1],
    ])
    res = {
        (0, 0): {(0, 1): 1},
        (0, 1): {??},
        (0, 2): {??},
        (2, 0): {(2, 1): 1},
        (2, 1): {(2, 0): 1},
    }
    assert maze_to_succdict(maze) == res

teste_maze_to_succdict()

3. Files et piles

Le code ci-dessous illustre l'utilisation de la structure de données deque du module collections en temps que pile (appelées stack en anglais, aussi appelées structure LIFO pour "last in first out"). Compléter le code suivant afin que tous les test passent avec succès.

from collections import deque

def teste_deque_comme_pile():
    dq = deque([6, 5])
    dq.append(9)
    dq.append(4)
    assert dq.pop() == ??
    assert len(dq) == ??
    dq.pop()
    assert len(dq) == ??
    assert dq.pop() == ??
    dq.pop()
    assert len(dq) == ??

teste_deque_comme_pile()

4. Parcours en profondeur

Un parcours de graphe est dit en profondeur si pour chaque sommet

il visite ce sommet;
puis visite récursivement chaque sommet adjacent non déjà parcouru.

Ainsi

c'est un parcours qui s'implément facilement de façon récursive;
les sommets fils sont parcourus avant les frères (sauf pour les fils qui ont déjà été parcourus et ne se donc pas reparcourus).
on peut vouloir effectuer une action en rentrant dans un sommet (donc avant de visiter les fils non encore visités) par exemple si on veut créer une hierarchie de dossiers/sous-dossiers non a partir de sa représentation sous forme de graphe;

on peut vouloir effectuer une action en sortant d'un sommet (donc après avoir visité tous ses fils) par exemple si on veut détruire une hierarchie de dossiers/sous-dossiers et qu'on ne peut supprimer que des dossiers vides.

En commençant votre script par le code ci-dessous

import os
import sys
from collections import deque

# Inutile de comprendre le fonctionnement de cette fonction: HP
def print_green(*args, **kwargs):
    OKGREEN = '\x1b[32m'
    ENDC = '\x1b[0m'
    print(*[OKGREEN+txt+ENDC for txt in args], **kwargs)

# Inutile de comprendre le fonctionnement de cette fonction: HP
def print_cyan(*args, **kwargs):
    OKCYAN = '\x1b[36m'
    ENDC = '\x1b[0m'
    print(*[OKCYAN+txt+ENDC for txt in args], **kwargs)

# Inutile de comprendre le fonctionnement de cette fonction: HP
def print_black(*args, **kwargs):
    print(*args, **kwargs)

def do_nothing(sommet):
    return

def previsite_print_sommet(sommet):
    print_green("Avant visite du sommet", sommet)

def postvisite_print_sommet(sommet):
    print_cyan("Après visite du sommet", sommet)

compléter le script suivant afin qu'il effectue un parcours en profondeur du graphe passé en premier argument

def parcours_profondeur_aux(G, sommet, previsite_fun, postvisite_fun, parent_dict):
    previsite_fun(sommet)
    for sommet_adj in ??:
        if ??: # sommet déjà visité?
            parent_dict[??] = ??
            parcours_profondeur_aux(??, ??, ??, ??, ??)
    postvisite_fun(sommet)

def parcours_profondeur(G, start, previsite_fun, postvisite_fun):
    parent_dict = {??: None}
    parcours_profondeur_aux(??, ??, ??, ??, ??)
    return parent_dict

Dans la suite on utilise le graphe ci-dessous

G_dict_dict = {
    "Chaos": ["Nyx", "Erebe", "Tartare", "Eros", "Gaya"],#
    "Nyx": ["Eris", "Hemera"],#
    "Erebe": ["Eris", "Hemera"],#
    "Gaya": ["Nymphes", "Ourea", "Pontos", "Ouranos"],#
    "Nymphes": [],#
    "Ourea": [],#
    "Pontos": [],#
    "Ouranos": ["Chronos", "Rhea"],#
    "Chronos": ["Zeus"],#
    "Rhea": ["Zeus"],#
    "Hemera": [],#
    "Eris": [],#
    "Erebe": [],#
    "Tartare": [],#
    "Eros": [],#
    "Chronos": [],#
    "Rhea": [],#
}     
draw_digraph_dict_of_list(G_dict_dict, layout="dot")

/tmp/ipykernel_41646/3099813051.py:11: DeprecationWarning: nx.nx_pydot.graphviz_layout depends on the pydot package, which has known issues and is not actively maintained. Consider using nx.nx_agraph.graphviz_layout instead.

See https://github.com/networkx/networkx/issues/5723
  pos = graphviz_layout(G, prog=layout, root=root)

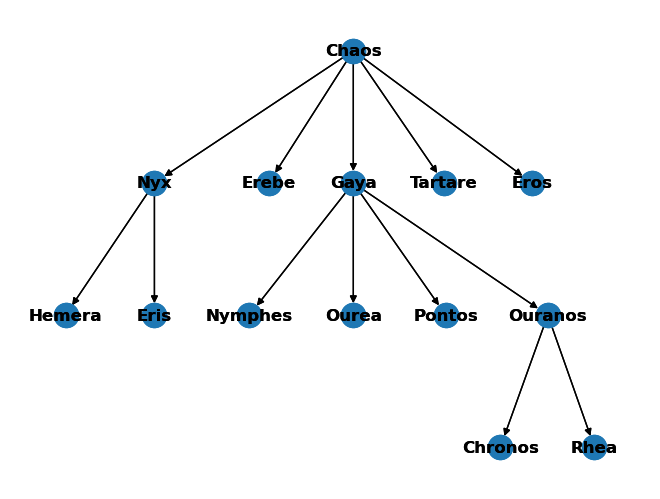
Vérifier que les scripts suivants donnent les sorties données dans la console.

```
print_black("Previsite (parcours en profondeur):")
parcours_profondeur(G_dict_dict, "Chaos", previsite_print_sommet, do_nothing)
```
: Previsite (parcours en profondeur):
Avant visite du sommet Chaos
Avant visite du sommet Nyx
Avant visite du sommet Eris
Avant visite du sommet Hemera
Avant visite du sommet Erebe
Avant visite du sommet Tartare
Avant visite du sommet Eros
Avant visite du sommet Gaya
Avant visite du sommet Nymphes
Avant visite du sommet Ourea
Avant visite du sommet Pontos
Avant visite du sommet Ouranos
Avant visite du sommet Chronos
Avant visite du sommet Rhea

```
print_black("Postvisite (parcours en profondeur):")
parcours_profondeur(G_dict_dict, "Chaos", do_nothing, postvisite_print_sommet)
```
: Postvisite (parcours en profondeur):
Après visite du sommet Eris
Après visite du sommet Hemera
Après visite du sommet Nyx
Après visite du sommet Erebe
Après visite du sommet Tartare
Après visite du sommet Eros
Après visite du sommet Nymphes
Après visite du sommet Ourea
Après visite du sommet Pontos
Après visite du sommet Chronos
Après visite du sommet Rhea
Après visite du sommet Ouranos
Après visite du sommet Gaya
Après visite du sommet Chaos
```
print_black("Previsite et postvisite  (parcours en profondeur):")
parcours_profondeur(G_dict_dict, "Chaos", previsite_print_sommet, postvisite_print_sommet)     
```
: Previsite et postvisite (parcours en profondeur):
Avant visite du sommet Chaos
Avant visite du sommet Nyx
Avant visite du sommet Eris
Après visite du sommet Eris
Avant visite du sommet Hemera
Après visite du sommet Hemera
Après visite du sommet Nyx
Avant visite du sommet Erebe
Après visite du sommet Erebe
Avant visite du sommet Tartare
Après visite du sommet Tartare
Avant visite du sommet Eros
Après visite du sommet Eros
Avant visite du sommet Gaya
Avant visite du sommet Nymphes
Après visite du sommet Nymphes
Avant visite du sommet Ourea
Après visite du sommet Ourea
Avant visite du sommet Pontos
Après visite du sommet Pontos
Avant visite du sommet Ouranos
Avant visite du sommet Chronos
Après visite du sommet Chronos
Avant visite du sommet Rhea
Après visite du sommet Rhea
Après visite du sommet Ouranos
Après visite du sommet Gaya
Après visite du sommet Chaos

5. Parcours en largeur

Un parcours de graphe est dit en largeur si les frères d'un sommet (non encore parcourus) sont parcourus avant ses fils (remarquons que cette décision a par contré été prise par le sommet parent car un sommet n'a pas accès directement à ses frêres).

En commençant votre script par le code ci-dessous

import os
import sys
from collections import deque

# Inutile de comprendre le fonctionnement de cette fonction: HP
def print_green(*args, **kwargs):
    OKGREEN = '\x1b[32m'
    ENDC = '\x1b[0m'
    print(*[OKGREEN+txt+ENDC for txt in args], **kwargs)

# Inutile de comprendre le fonctionnement de cette fonction: HP
def print_cyan(*args, **kwargs):
    OKCYAN = '\x1b[36m'
    ENDC = '\x1b[0m'
    print(*[OKCYAN+txt+ENDC for txt in args], **kwargs)

# Inutile de comprendre le fonctionnement de cette fonction: HP
def print_black(*args, **kwargs):
    print(*args, **kwargs)

def do_nothing(sommet):
    return

def previsite_print_sommet(sommet):
    print_green("Avant visite du sommet", sommet)

def postvisite_print_sommet(sommet):
    print_cyan("Après visite du sommet", sommet)

compléter le script suivant afin qu'il effectue nu parcours en profondeur du graphe passé en premier argument

def parcours_largeur(G, start, previsite_fun, postvisite_fun):
    parent_dict = ??
    parent_dict[??] = None
    dq = deque()
    dq.append(??)
    while len(??) ??:
        s = dq.popleft()
        previsite_fun(s)
        for adj in ??:
            if ??:
                parent_dict[??] = ??
                dq.append(??)
        postvisite_fun(s)
    return parent_dict

Dans la suite on utilise le graphe ci-dessous

G_dict_dict = {
    "Chaos": ["Nyx", "Erebe", "Tartare", "Eros", "Gaya"],#
    "Nyx": ["Eris", "Hemera"],#
    "Erebe": ["Eris", "Hemera"],#
    "Gaya": ["Nymphes", "Ourea", "Pontos", "Ouranos"],#
    "Nymphes": [],#
    "Ourea": [],#
    "Pontos": [],#
    "Ouranos": ["Chronos", "Rhea"],#
    "Chronos": ["Zeus"],#
    "Rhea": ["Zeus"],#
    "Hemera": [],#
    "Eris": [],#
    "Erebe": [],#
    "Tartare": [],#
    "Eros": [],#
    "Chronos": [],#
    "Rhea": [],#
}     
draw_digraph_dict_of_list(G_dict_dict, layout="dot")

/tmp/ipykernel_41646/3099813051.py:11: DeprecationWarning: nx.nx_pydot.graphviz_layout depends on the pydot package, which has known issues and is not actively maintained. Consider using nx.nx_agraph.graphviz_layout instead.

See https://github.com/networkx/networkx/issues/5723
  pos = graphviz_layout(G, prog=layout, root=root)

Vérifier que les scripts suivants donnent les sorties données dans la console. Vérifier que les scripts suivants donnent les sorties données dans la console.

```
print_black("Previsite  (parcours en largeur):")
parcours_largeur(G_dict_dict, "Chaos", previsite_print_sommet, do_nothing)
```
: Previsite (parcours en largeur):
Avant visite du sommet Chaos
Avant visite du sommet Nyx
Avant visite du sommet Erebe
Avant visite du sommet Tartare
Avant visite du sommet Eros
Avant visite du sommet Gaya
Avant visite du sommet Eris
Avant visite du sommet Hemera
Avant visite du sommet Nymphes
Avant visite du sommet Ourea
Avant visite du sommet Pontos
Avant visite du sommet Ouranos
Avant visite du sommet Chronos
Avant visite du sommet Rhea
```
print_black("Postvisite (parcours en largeur):")
parcours_largeur(G_dict_dict, "Chaos", do_nothing, postvisite_print_sommet)
```
: Postvisite (parcours en largeur):
Après visite du sommet Chaos
Après visite du sommet Nyx
Après visite du sommet Erebe
Après visite du sommet Tartare
Après visite du sommet Eros
Après visite du sommet Gaya
Après visite du sommet Eris
Après visite du sommet Hemera
Après visite du sommet Nymphes
Après visite du sommet Ourea
Après visite du sommet Pontos
Après visite du sommet Ouranos
Après visite du sommet Chronos
Après visite du sommet Rhea
```
print_black("Previsite et postvisite (parcours en largeur):")
parcours_largeur(G_dict_dict, "Chaos", previsite_print_sommet, postvisite_print_sommet)     
```
: Previsite et postvisite (parcours en largeur):
Avant visite du sommet Chaos
Après visite du sommet Chaos
Avant visite du sommet Nyx
Après visite du sommet Nyx
Avant visite du sommet Erebe
Après visite du sommet Erebe
Avant visite du sommet Tartare
Après visite du sommet Tartare
Avant visite du sommet Eros
Après visite du sommet Eros
Avant visite du sommet Gaya
Après visite du sommet Gaya
Avant visite du sommet Eris
Après visite du sommet Eris
Avant visite du sommet Hemera
Après visite du sommet Hemera
Avant visite du sommet Nymphes
Après visite du sommet Nymphes
Avant visite du sommet Ourea
Après visite du sommet Ourea
Avant visite du sommet Pontos
Après visite du sommet Pontos
Avant visite du sommet Ouranos
Après visite du sommet Ouranos
Avant visite du sommet Chronos
Après visite du sommet Chronos
Avant visite du sommet Rhea
Après visite du sommet Rhea

Écrire une fonction liste_sommets_sans_dup

def liste_sommets_sans_dup(G):
    L = ??
    for s in G:
        if ??:
            L.append(??)
        for adj in ??:
            if ??:
                L.append(??)
    return ??

def test_liste_sommets_sans_dup():
    G = {"A": ["B"]}
    res = liste_sommets_sans_dup(G)
    assert res == ["A", "B"] or res == ["B", "A"]
    G = {"A": [], "B": []}
    res = liste_sommets_sans_dup(G)
    assert res == ["A", "B"] or res == ["B", "A"]

test_liste_sommets_sans_dup()

On souhaite utiliser un parcours en largeur pour vérifier si un graphe non orienté est connexe ou non.

Écrire une fonction est_symetrique

def est_symetrique(G):
    for s in G:
        for s_adj in ??:
            if ??:
                return ??
    return return ??

def test_est_symetrique():
    G = {"A": ["B"]}
    assert not est_symetrique(G)
    G = {"A": ["B"], "B": ["A"]}
    assert est_symetrique(G)
    G = {"A": ["B", "C"], "B": ["A"], "C": ["A"]}
    assert est_symetrique(G)

test_est_symetrique()

À l'aide d'un parcours en largeur écrire une fonction est_connexe qui accepte un graphe non orienté (on verifiera que ce graphe est bien non orienté) et qui retourne True ou False suivant que ce graphe est ou non connexe.

6. Applications aux parcours de labyrinthes

G = maze_to_succdict(maze)
maze = np.array([
    #0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], #  0
    [0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0], #  1
    [0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0], #  2
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0], #  3
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1], #  4
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0], #  5
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0], #  6
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0], #  7
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1], #  8
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0], #  9
    [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0], # 10
    [0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0], # 11
])

En résolvant le labyrinthe via un parcours en profondeur vérifier que le code ci-dessous vous donne le graphique qui lui suit

G = maze_to_succdict(maze)
start_list = [(11,0), (3,12)]
fig, axs = plt.subplots(1, 2)
fig.suptitle('Parcours en largeur', fontsize=16)
goal = (0,0)
for i in range(len(start_list)):
    start = start_list[i]
    parent_dict = parcours_profondeur(G, start, do_nothing, do_nothing)
    path = create_path_using_parent_dict(parent_dict, goal)
    plot_maze_and_paths(maze, [path], ax=axs[i])
plt.show()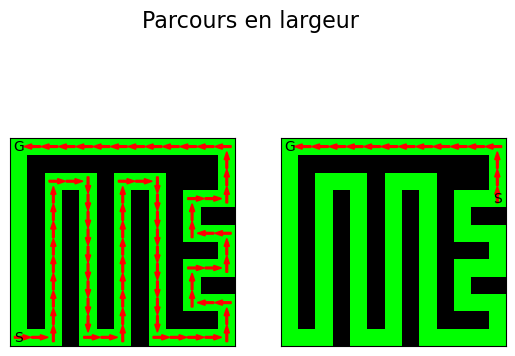

En résolvant le labyrinthe via un parcours en largeur cette fois vérifier que le code ci-dessous vous donne le graphique qui lui suit

G = maze_to_succdict(maze)
start_list = [(11,0), (3,12)]
fig, axs = plt.subplots(1, 2)
fig.suptitle('Parcours en largeur', fontsize=16)
goal = (0,0)
for i in range(len(start_list)):
    start = start_list[i]
    parent_dict = parcours_largeur(G, start, do_nothing, do_nothing)
    path = create_path_using_parent_dict(parent_dict, goal)
    plot_maze_and_paths(maze, [path], ax=axs[i])
plt.show()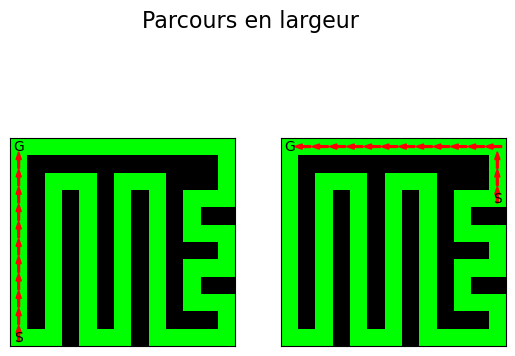

Vaut-il mieux utiliser un parcours en largeur ou en profondeur pour résoudre un labyrinthe?

7. Cycles et connexité dans un graphe non orienté

un graphe non orienté est dite connexe si tout sommet peut être atteint à partir d'un autre.
Le fait qu'un graphe non orienté possède un cycle peut être détecté lors d'un parcours, de préference lors d'un parcours en profondeur.
1. Écrire une fonction graphe_est_connexe qui accepte une matrice d'adjacence en argument (représentée par une liste de liste d'entiers ou par un tableau numpy) et qui en effectuant un parcourt en profondeur retourne True si le graphe est connexe et False sinon.
2. Écrire une fonction graphe_non_orienté_a_cycle qui accepte une matrice d'adjacence en argument (représentée par une liste de liste d'entiers ou par un tableau numpy) et qui en effectuant un parcourt en profondeur retourne True si le graphe possède un cycle et False sinon.